Evaluates a sequence of Bessel functions of the second kind with real order and complex arguments.

Required Arguments

XNU — Real argument which is the lowest order desired.   (Input)
XNU must be greater than −1/2.

Z — Complex argument for which the sequence of Bessel functions is to be evaluated.   (Input)

N — Number of elements in the sequence.   (Input)

CBS — Vector of length N containing the values of the function through the series.   (Output)
CBS(I) contains the value of the Bessel function of order XNU + I − 1 at Z for I = 1
to N.

FORTRAN 90 Interface

Generic:                              CALL CBYS (XNU, Z, N, CBS)

Specific:                             The specific interface names are S_CBYS and D_CBYS.

FORTRAN 77 Interface

Single:                                CALL CBYS (XNU, Z, N, CBS)

Double:                              The double precision name is DCBYS.

Description

The Bessel function Yν(z) is defined to be

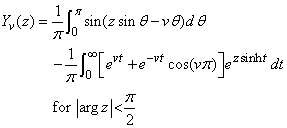
This code is based on the code BESSEC of Barnett (1981) and Thompson and Barnett (1987).

This code computes Yν(z) from the modified Bessel functions Iν(z) and Kν(z), CBIS and CBKS, using the following relation:

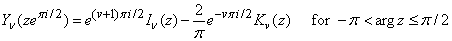
Comments

1.         Workspace may be explicitly provided, if desired, by use of C2YS/DC2Y. The reference is:

CALL C2YS (XNU, Z, N, CBS, FK)

The additional argument is:

FK — complex work vector of length N.

2.         Informational errors

Type Code

3         1                  One of the continued fractions failed.

4         2                  Only the first several entries in CBS are valid.

Example

In this example, Y0.3+ν−1(1.2 + 0.5i), ν= 1, …, 4 is computed and printed.

 

      USE CBYS_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

!                                 Declare variables

      INTEGER    N

      PARAMETER  (N=4)

!    

      INTEGER    K, NOUT

      REAL       XNU

      COMPLEX    CBS(N), Z

!                                 Compute

      XNU = 0.3

      Z   = (1.2, 0.5)

      CALL CBYS (XNU, Z, N, CBS)

!                                 Print the results

      CALL UMACH (2, NOUT)

      DO 10  K=1, N

         WRITE (NOUT,99999) XNU+K-1, Z, CBS(K)

   10 CONTINUE

99999 FORMAT (' Y sub ', F6.3, ' ((', F6.3, ',', F6.3, &

           ')) = (', F9.3, ',', F9.3, ')')

      END

Output

 

 Y sub  0.300 (( 1.200, 0.500)) = (   -0.013,    0.380)

 Y sub  1.300 (( 1.200, 0.500)) = (   -0.716,    0.338)

 Y sub  2.300 (( 1.200, 0.500)) = (   -1.048,    0.795)

 Y sub  3.300 (( 1.200, 0.500)) = (   -1.625,    3.684)

http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260