This function evaluates the chi-squared probability density function.
Function Return Value
CHIPR — Function value, the value of the probability density function. (Output)
Required Arguments
X — Argument for which the chi-squared probability density function is to be evaluated. (Input)
DF — Number of degrees of freedom of the chi-squared distribution. (Input)
FORTRAN 90 Interface
Generic: CHIPR (X, DF)
Specific: The specific interface names are S_CHIPR and D_CHIPR.
FORTRAN 77 Interface
Single: CHIPR (X, DF)
Double: The double precision name is DCHIPR.
Description
The function CHIPR evaluates the chi-squared probability density function. The chi-squared distribution is a special case of the gamma distribution and is defined as
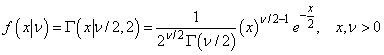 .
.
Example
In this example, we evaluate the probability function at X = 3.0, DF = 5.0.
USE
UMACH_INT
USE
CHIPR_INT
IMPLICIT NONE
INTEGER NOUT
REAL X, DF, PR
CALL UMACH(2, NOUT)
X = 3.0
DF = 5.0
PR = CHIPR(X, DF)
WRITE (NOUT, 99999) X, DF, PR
99999 FORMAT (' CHIPR(', F4.2, ', ', F4.2, ') = ', F6.4)
END
Output
CHIPR(3.00, 5.00) = 0.1542
|
PHONE: 713.784.3131 FAX:713.781.9260 |