This function evaluates the Weierstrass' ℘ function in the equianharmonic case for complex argument with unit period parallelogram.
Function Return Value
CWPQ — Complex function value. (Output)
Required Arguments
Z — Complex argument for which the function value is desired. (Input)
FORTRAN 90 Interface
Generic: CWPQ (Z)
Specific: The specific interface names are C_CWPQ and Z_CWPQ.
FORTRAN 77 Interface
Complex: CWPQ (Z)
Double complex: The double complex name is ZWPQ.
Description
The Weierstrass' ℘ function, ℘(z) = ℘(z | ω, ωʹ), is an elliptic function of order two with periods 2ω and 2 ωʹ and a double pole at z = 0. CWPQ(Z) computes ℘(z | ω, ωʹ) with
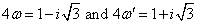
The input argument is first reduced to the fundamental parallelogram of all z satisfying
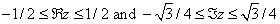
Then, a rational approximation is used.
All arguments are valid with the exception of the lattice points
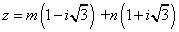
which are the poles of CWPQ. If the argument is a lattice point, then b = AMACH(2), the largest floating-point number, is returned. If the argument has modulus greater than 10 ε−1, then NaN (not a number) is returned. Here, ε = AMACH(4) is the machine precision.
Function CWPQ is based on code by Eckhardt (1980). Also, see Eckhardt (1977).
Example
In this example, ℘(0.25 + 0.14437567i) is computed and printed.
USE CWPQ_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER NOUT
COMPLEX VALUE, Z
! Compute
Z = (0.25, 0.14437567)
VALUE = CWPQ(Z)
! Print the results
CALL UMACH (2, NOUT)
WRITE (NOUT,99999) Z, VALUE
99999 FORMAT (' CWPQ(', F6.3, ',', F6.3, ') = (', &
F7.3, ',', F7.3, ')')
END
Output
CWPQ( 0.250, 0.144) = ( 5.895,-10.216)
|
PHONE: 713.784.3131 FAX:713.781.9260 |