This function evaluates an elementary integral from which inverse circular functions, logarithms and inverse hyperbolic functions can be computed.
Function Return Value
ELRC — Function value. (Output)
Required Arguments
X — First
variable of the incomplete elliptic integral. (Input)
It must be
nonnegative and satisfy the conditions given in Comments.
Y — Second
variable of the incomplete elliptic integral. (Input)
It must be
positive and satisfy the conditions given in Comments.
FORTRAN 90 Interface
Generic: ELRC (X, Y)
Specific: The specific interface names are S_ELRC and D_ELRC.
FORTRAN 77 Interface
Single: ELRC (X, Y)
Double: The double precision name is DELRC.
Description
The special case of Carlson's complete elliptic integral of the first kind is defined to be
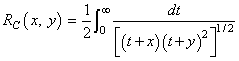
The argument x must be nonnegative, y must be positive, and x + y must be less than or equal to b/5 and greater than or equal to 5s. If any of these conditions are false, then ELRC is set to b. Here, b = AMACH(2) is the largest and s = AMACH(1) is the smallest representable floating-point number.
The function ELRC is based on the code by Carlson and Notis (1981) and the work of Carlson (1979).
Comments
The sum X + Y must be greater than or equal to ARGMIN and both X and Y must be less than or equal to ARGMAX. ARGMIN = s * 5 and ARGMAX = b/5, where s is the machine minimum (AMACH(1)) and b is the machine maximum (AMACH(2)).
Example
In this example, RC(2.25, 2.0) is computed and printed.
USE ELRC_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER NOUT
REAL VALUE, X, Y
! Compute
X = 0.0
Y = 1.0
VALUE = ELRC(X, Y)
! Print the results
CALL UMACH (2, NOUT)
WRITE (NOUT,99999) X, Y, VALUE
99999 FORMAT (' ELRC(', F6.3, ',', F6.3, ') = ', F6.3)
END
Output
ELRC( 0.000, 1.000) = 1.571
|
PHONE: 713.784.3131 FAX:713.781.9260 |