This function evaluates Carlson's incomplete elliptic integral of the first kind RF(X, Y, Z).
Function Return Value
ELRF — Function value. (Output)
Required Arguments
X — First
variable of the incomplete elliptic integral. (Input)
It must be
nonnegative
Y — Second
variable of the incomplete elliptic integral. (Input)
It must be
nonnegative.
Z — Third
variable of the incomplete elliptic integral. (Input)
It must be
nonnegative.
FORTRAN 90 Interface
Generic: ELRF (X, Y, Z)
Specific: The specific interface names are S_ELRF and D_ELRF.
FORTRAN 77 Interface
Single: ELRF (X, Y, Z)
Double: The double precision name is DELRF.
Description
The Carlson's complete elliptic integral of the first kind is defined to be
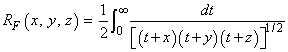
The arguments must be nonnegative and less than or equal to
b/5. In addition, x + y, x + z, and
y + z must be greater than or equal to 5s. Should any
of these conditions fail, ELRF
is set to b. Here, b = AMACH(2)
is the largest and s = AMACH(1)
is the smallest representable floating-point number.
The function ELRF is based on the code by Carlson and Notis (1981) and the work of Carlson (1979).
Example
In this example, RF(0, 1, 2) is computed and printed.
USE ELRF_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER NOUT
REAL VALUE, X, Y, Z
! Compute
X = 0.0
Y = 1.0
Z = 2.0
VALUE = ELRF(X, Y, Z)
! Print the results
CALL UMACH (2, NOUT)
WRITE (NOUT,99999) X, Y, Z, VALUE
99999 FORMAT (' ELRF(', F6.3, ',', F6.3, ',', F6.3, ') = ', F6.3)
END
Output
ELRF( 0.000, 1.000, 2.000) = 1.311
|
PHONE: 713.784.3131 FAX:713.781.9260 |