This function evaluates the noncentral F cumulative distribution function (CDF).
Function Return Value
FNDF — Probability that a random variable from an F distribution having noncentrality parameter LAMBDA takes a value less than or equal to the input F. (Output)
Required Arguments
F — Argument for
which the noncentral F cumulative distribution function is to be
evaluated. (Input)
F must be non-negative.
DF1 — Number of
numerator degrees of freedom of the noncentral F
distribution. (Input)
DF1 must be positive.
DF2 — Number of
denominator degrees of freedom of the noncentral F
distribution. (Input)
DF2 must be positive.
LAMBDA —
Noncentrality parameter. (Input)
LAMBDA must be non-negative.
FORTRAN 90 Interface
Generic: FNDF (F, DF1, DF2, LAMBDA)
Specific: The specific interface names are S_FNDF and D_FNDF.
Description
If X is a noncentral chi-square random variable with noncentrality parameter λ and ν1 degrees of freedom, and Y is a chi-square random variable with ν2 degrees of freedom which is statistically independent of X, then
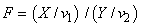
is a noncentral F-distributed random variable whose CDF is given by
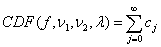
where
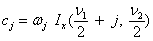
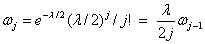
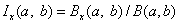
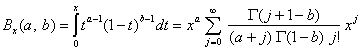
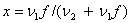
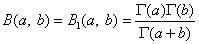
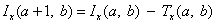
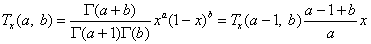
and Γ(.) is the gamma function. The above series expansion for the noncentral F CDF was taken from Butler and Paolella (1999) (see Paolella.pdf), with the correction for the recursion relation given below:
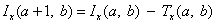
extracted from the AS 63 algorithm for calculating the incomplete beta function as described by Majumder and Bhattacharjee (1973).
The correspondence between the arguments of function FNDF(F, DF1, DF2, LAMBDA) and the variables in the above equations is as follows: ν1 = DF1, ν2 = DF2, λ = LAMBDA, and f = F.
For λ = 0, the noncentral F distribution is the same as the F distribution.
Example
This example traces out a
portion of a noncentral F distribution with parameters  .
.
USE UMACH_INT
USE FNDF_INT
IMPLICIT NONE
INTEGER NOUT, I
REAL X, LAMBDA, DF1, DF2, CDFV, X0(8)
DATA X0 / 0.0, .4, .8, 1.2, 1.6, 2.0, 2.8, 4.0 /
CALL UMACH (2, NOUT)
DF1 = 100.0
DF2 = 10.0
LAMBDA = 10.0
WRITE (NOUT,'("DF1: ", F4.0, "; DF2: ", F4.0, &
"; LAMBDA: ", F4.0 // " X CDF(X)")')&
DF1, DF2, LAMBDA
DO I = 1, 8
X = X0(I)
CDFV = FNDF(X, DF1, DF2, LAMBDA)
WRITE (NOUT,'(1X, F5.1, 2X, E12.6)') X, CDFV
END DO
END
Output
DF1: 100.; DF2: 10.; LAMBDA: 10.
X CDF(X)
0.0 0.000000E+00
0.4 0.488790E-02
0.8 0.202633E+00
1.2 0.521143E+00
1.6 0.733853E+00
2.0 0.850413E+00
2.8 0.947125E+00
4.0 0.985358E+00
|
PHONE: 713.784.3131 FAX:713.781.9260 |