This function evaluates a generalization of Pochhammer's symbol starting from the first order.

Function Return Value

POCH1 — Function value.   (Output)
POCH1(A, X) = (POCH(A, X) − 1)/X.

Required Arguments

A — The first argument.   (Input)

X — The second, differential argument.   (Input)

FORTRAN 90 Interface

Generic:                              POCH1 (A, X)

Specific:                             The specific interface names are S_POCH1 and D_POCH1.

FORTRAN 77 Interface

Single:                                POCH1 (A, X)

Double:                              The double precision function name is DPOCH1.

Description

Pochhammer's symbol from the first order is defined to be

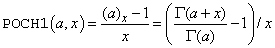
where (a)x is Pochhammer's generalized symbol. See POCH for the definition of (a)x. It is useful in special situations that require especially accurate values when x is small. This specification is particularly suited for stability when computing expressions such as

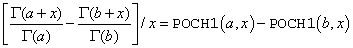
Note that POCH1(a, 0) = ψ(a). See PSI for the definition of ψ(a).

When |x| is so small that substantial cancellation will occur if the straightforward formula is used, we use an expansion due to fields and discussed by Luke (1969).

The ratio (a)x = Γ(a + x)/ Γ(a) is written by Luke as (a + (x − 1)/2)x times a polynomial in
(a + (x − 1)/2)⁻². To maintain significance in POCH1, we write for positive a,

(a + (x − 1)/2)x = exp(x ln(a + (x − 1)/2)) = eq = 1 + qEXPRL(q)

where EXPRL(x) = (ex − 1)/x. Likewise, the polynomial is written P = 1 + xP1 (a, x). Thus,

POCH1 (a, x) = ((a)x − 1)/x = EXPRL(q)(q/x + qP1(a, x)) + P1(a, x)

Substantial significance loss can occur if a + x or a are close to a negative integer even when |x| is very small. To insure that the result does not overflow or underflow, one can keep the arguments a and a + x well within the range dictated by the gamma function routine GAMMA or one can keep |x| small whenever a is large. POCH also works for a variety of arguments outside these rough limits, but any more general limits that are also useful are difficult to specify.

Example

In this example, POCH1(1.6, 0.8) is computed and printed.

 

      USE POCH1_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

!                                 Declare variables

      INTEGER    NOUT

      REAL       A, VALUE, X

!                                 Compute

      A     = 1.6

      X     = 0.8

      VALUE = POCH1(A, X)

!                                 Print the results

      CALL UMACH (2, NOUT)

      WRITE (NOUT,99999) A, X, VALUE

99999 FORMAT (' POCH1(', F6.3, ',', F6.3, ') = ', F6.4)

      END

Output

 

POCH1( 1.600, 0.800) = 0.4878

http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260