This function evaluates the noncentral Student's t probability density function.
Function Return Value
TNPR — Function value, the value of the probability density function. (Output)
Required Arguments
T — Argument for which the noncentral Student's t probability density function is to be evaluated. (Input)
DF — Number of
degrees of freedom of the noncentral Student's
t distribution. (Input)
DF must be positive.
DELTA — Noncentrality parameter. (Input)
FORTRAN 90 Interface
Generic: TNPR (T, DF, DELTA)
Specific: The specific interface names are S_TNPR and D_TNPR.
Description
The noncentral Student's t distribution is a generalization of the Student's t distribution.
If w is a normally distributed random variable with unit variance and mean δ and u is a chi-square random variable with ν degrees of freedom that is statistically independent of w, then

is a noncentral t-distributed random variable with ν degrees of freedom and noncentrality parameter δ, that is, with v = DF, and δ = DELTA. The probability density function for the noncentral t-distribution is:
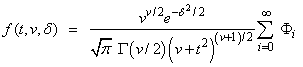
where
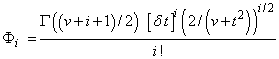
and t = T.
For δ = 0, the PDF reduces to the (central) Student's t PDF:
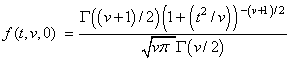
and, for t = 0, the PDF becomes:
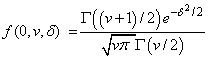
Example
This example calculates the noncentral Student's t PDF for a distribution with 2 degrees of freedom and noncentrality parameter δ = 10.
USE TNPR_INT
USE UMACH_INT
IMPLICIT NONE
INTEGER :: NOUT, I
REAL :: X(6)=(/ -.5, 1.5, 3.5, 7.5, 51.5, 99.5 /)
REAL :: DF, DELTA, PDFV
CALL UMACH (2, NOUT)
DF = 2.0
DELTA = 10.0
WRITE (NOUT,'("DF: ", F4.0, " DELTA: ", F4.0 //' // &
' " X PDF(X)")') DF, DELTA
DO I = 1, 6
PDFV = TNPR(X(I), DF, DELTA)
WRITE (NOUT,'(1X, F4.1, 2X, E12.5)') X(I), PDFV
END DO
END
Output
DF: 2. DELTA: 10.
X PDF(X)
-0.5 0.16399E-23
1.5 0.74417E-09
3.5 0.28972E-02
7.5 0.78853E-01
51.5 0.14215E-02
99.5 0.20290E-03
|
PHONE: 713.784.3131 FAX:713.781.9260 |