Usage Notes
Many functions of one variable can be numerically computed using a Chebyshev series,
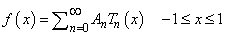
A Chebyshev series is better for numerical computation than a Taylor series since the Chebyshev polynomials, Tn(x), are better behaved than the monomials, xn.
A Taylor series can be converted into a Chebyshev series using an algorithm of Fields and Wimp, (see Luke (1969), page 292).
Let
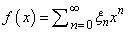
be a Taylor series expansion valid for |x| < 1. Define
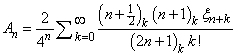
where (a)k = Γ(a + k)/Γ(a) is Pochhammer's symbol.
(Note that (a)k+1 = (a + k)(a)k). Then,
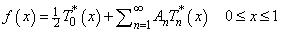
where
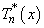
are the shifted Chebyshev polynomials,
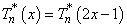
In an actual implementation of this algorithm, the number of terms in the Taylor series and the number of terms in the Chebyshev series must both be finite. If the Taylor series is an alternating series, then the error in using only the first M terms is less than |ξM +1|. The error in truncating the Chebyshev series to N terms is no more than
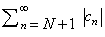
If the Taylor series is valid on |x| < R, then we can write
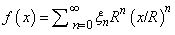
and use ξnRn instead of ξn in the algorithm to obtain a Chebyshev series in x/R valid for 0 < x < R. Unfortunately, if R is large, then the Chebyshev series converges more slowly.
The Taylor series centered at zero can be shifted to a Taylor series centered at c. Let t = x − c, so
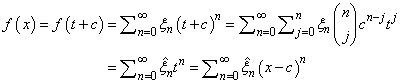
By interchanging the order of the double sum, it can easily be shown that
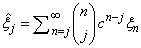
By combining scaling and shifting, we can obtain a Chebyshev series valid over any interval [a, b] for which the original Taylor series converges.
The algorithm can also be applied to asymptotic series,
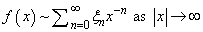
by treating the series truncated to M terms as a
polynomial in 1/x. The asymptotic series is usually divergent; but if it
is alternating, the error in truncating the series to M terms is less
than 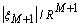 for R ≤
x < ∞. Normally, as M increases, the error initially decreases
to a small value and then increases without a bound. Therefore, there is a limit
to the accuracy that can be obtained by increasing M. More accuracy can
be obtained by increasing R. The optimal value of M depends on
both the sequence ξj and R. For
R fixed, the optimal value of M can be found by finding the value
of M at which
for R ≤
x < ∞. Normally, as M increases, the error initially decreases
to a small value and then increases without a bound. Therefore, there is a limit
to the accuracy that can be obtained by increasing M. More accuracy can
be obtained by increasing R. The optimal value of M depends on
both the sequence ξj and R. For
R fixed, the optimal value of M can be found by finding the value
of M at which 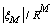 starts to increase.
starts to increase.
Since we want a routine accurate to near machine precision, the algorithm must be implemented using somewhat higher precision than is normally used. This is best done using a symbolic computation package.
|
PHONE: 713.784.3131 FAX:713.781.9260 |