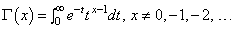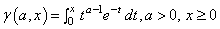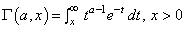FAC

n! = Γ(n + 1)

BINOM

n!/m!(n - m)!, 0 ≤ m ≤ n

GAMMA

GAMR

1/ Γ(x)

ALNGAM

ln ǀΓ(x)ǀ, x ≠ 0, -1, -2, …

ALGAMS

ln ǀΓ(x)ǀ and sign Γ(x), x ≠ 0, -1, -2, …

GAMI

GAMIC

GAMIT

γ*(a, x) = (x⁻¹a/ Γ(a))γ(a, x), x ≥ 0

PSI

ψ(x) = Γ´(x)/ Γ(x), x ≠ 0, -1, -2, …

PSI1

ψ1(x) =d²/dx² ln Γ(x), x ≠ 0, -1, -2, …

POCH

(a)x = Γ(a + x)/ Γ(a), if a + x = 0, -1, -2, … then a must = 0, -1, -2, …

POCH1

((a)x - 1)/x, if a + x = 0, -1, -2, … then a must = 0, -1, -2, …

BETA

β(x1, x2) = Γ(x1) Γ(x2)/ Γ(x1 + x2), x1 > 0 and x2 > 0

CBETA

β(z1, z2) = Γ(z1) Γ(z2)/ Γ(z1 + z2), z1 > 0 and z2 > 0

ALBETA

ln β(a, b), a > 0, b > 0

BETAI

Ix(a, b) = βx(a, b)/ β(a, b), 0 ≤ x ≤ 1, a > 0, b > 0