The notation used in this chapter follows that of Abramowitz and Stegun (1964) and Carlson (1979).

The complete elliptic integral of the first kind is

 

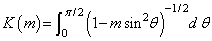
and the complete elliptic integral of the second kind is

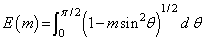
Instead of the parameter m, the modular angle α is sometimes used with m = sin2 α. Also used is the modulus k with k2 = m.

 

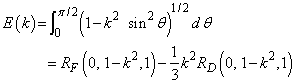
Carlson Elliptic Integrals

The Carlson elliptic integrals are defined by Carlson (1979) as follows:

 

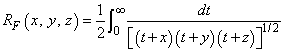
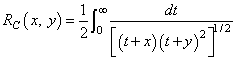
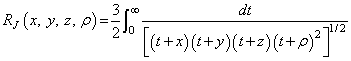
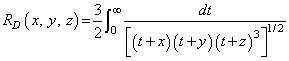
The standard Legendre elliptic integrals can be written in terms of the Carlson functions as follows (these relations are from Carlson (1979)):

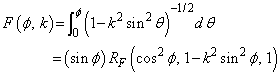
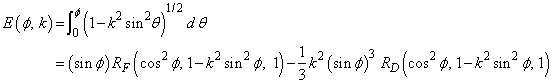
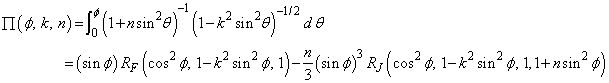
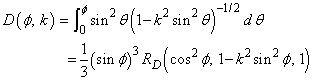
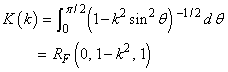
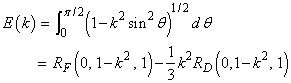
The function RC(x, y) is related to inverse trigonometric and inverse hyperbolic functions.

 

http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260