ANORDF

This function evaluates the standard normal (Gaussian) cumulative distribution function.

Function Return Value

ANORDF — Function value, the probability that a normal random variable takes a value less than or equal to X. (Output)

Required Arguments

X — Argument for which the normal cumulative distribution function is to be evaluated. (Input)

FORTRAN 90 Interface

Generic: ANORDF (X)

Specific: The specific interface names are S_ANORDF and D_ANORDF.

FORTRAN 77 Interface

Single: ANORDF (X)

Double: The double precision name is DNORDF.

Description

Function ANORDF evaluates the cumulative distribution function, Φ, of a standard normal (Gaussian) random variable, that is,

 

The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.

The standard normal distribution (for which ANORDF is the distribution function) has mean of 0 and variance of 1. The probability that a normal random variable with mean μ and variance σ2 is less than y is given by ANORDF evaluated at (y ‑ μ)/σ.

Φ(x) is evaluated by use of the complementary error function, erfc. (See ERFC, IMSL MATH/LIBRARY Special Functions). The relationship is:

 

 

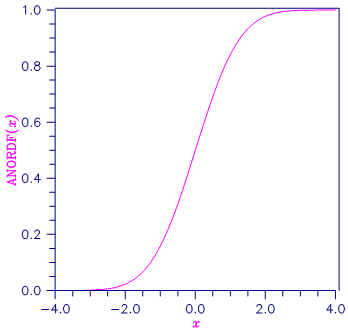
Figure 1,  Standard Normal Distribution Function

Example

Suppose X is a normal random variable with mean 100 and variance 225. In this example, we find the probability that X is less than 90, and the probability that X is between 105 and 110.

 

USE UMACH_INT

USE ANORDF_INT

IMPLICIT NONE

INTEGER NOUT

REAL P, X1, X2

!

CALL UMACH (2, NOUT)

X1 = (90.0-100.0)/15.0

P = ANORDF(X1)

WRITE (NOUT,99998) P

99998 FORMAT (' The probability that X is less than 90 is ', F6.4)

X1 = (105.0-100.0)/15.0

X2 = (110.0-100.0)/15.0

P = ANORDF(X2) - ANORDF(X1)

WRITE (NOUT,99999) P

99999 FORMAT (' The probability that X is between 105 and 110 is ', &

F6.4)

END

Output

 

The probability that X is less than 90 is 0.2525

The probability that X is between 105 and 110 is 0.1169