PACF

Computes the sample partial autocorrelation function of a stationary time series.

Required Arguments

MAXLAG — Maximum lag of partial autocorrelations to be computed. (Input)

AC — Vector of length MAXLAG+ 1 containing the autocorrelations of the time series X. (Input)
AC(0) = 1. AC(k) contains the autocorrelation of lag k where k = 1, …, MAXLAG.

PAC — Vector of length MAXLAG containing the partial autocorrelations of the time series X. (Output)
The partial autocorrelation of lag k corresponds to PAC(k) where k = 1, …, MAXLAG.

FORTRAN 90 Interface

Generic: CALL PACF (MAXLAG, AC, PAC)

Specific: The specific interface names are S_PACF and D_PACF.

FORTRAN 77 Interface

Single: CALL PACF (MAXLAG, AC, PAC)

Double: The double precision name is DPACF.

Description

Routine PACF estimates the partial autocorrelations of a stationary time series given the
K = MAXLAG sample autocorrelations

 

for k = 0, 1, …, K. Consider the AR(k) process defined by

 

where ɸkj denotes the j‑th coefficient in the process. The set of estimates

 

for k = 1, …, K is the sample partial autocorrelation function. The autoregressive parameters

 

for j = 1, …, k are approximated by Yule‑Walker estimates for successive AR(k) models where k = 1, …, K. Based on the sample Yule‑Walker equations

 

a recursive relationship for k = 1, …, K was developed by Durbin (1960). The equations are given by

 

 

and

 

 

This procedure is sensitive to rounding error and should not be used if the parameters are near the nonstationarity boundary. A possible alternative would be to estimate { ɸkk} for successive AR(k) models using least squares (IMSL routine NSLSE) or maximum likelihood. Based on the hypothesis that the true process is AR(p), Box and Jenkins (1976, page 65) note

 

See Box and Jenkins (1976, pages 82–84) for more information concerning the partial autocorrelation function.

Comments

Workspace may be explicitly provided, if desired, by use of P2CF/DP2CF. The reference is:

CALL P2CF (MAXLAG, AC, PAC, WK)

The additional argument is:

WK — Work vector of length 2 * MAXLAG.

Example

Consider the Wolfer Sunspot Data (Anderson 1971, page 660) consisting of the number of sunspots observed each year from 1749 through 1924. The data set for this example consists of the number of sunspots observed from 1770 through 1869. Routine PACF to used to compute the estimated partial autocorrelations.

 

USE GDATA_INT

USE ACF_INT

USE PACF_INT

USE WRRRL_INT

 

IMPLICIT NONE

INTEGER IMEAN, IPRINT, ISEOPT, MAXLAG, NOBS

PARAMETER (IMEAN=1, IPRINT=0, ISEOPT=0, MAXLAG=20, NOBS=100)

!

INTEGER NCOL, NROW

REAL AC(0:MAXLAG), ACV(0:MAXLAG), PAC(MAXLAG), &

RDATA(176,2), SEAC(1), X(NOBS), XMEAN

CHARACTER CLABEL(2)*4, RLABEL(1)*6

!

EQUIVALENCE (X(1), RDATA(22,2))

!

DATA RLABEL/'NUMBER'/, CLABEL/'Lag ', 'PACF'/

! Wolfer Sunspot Data for

! years 1770 through 1869

CALL GDATA (2, RDATA, NROW, NCOL)

! Compute sample ACF

CALL ACF (X, MAXLAG, AC)

! Compute sample PACF

CALL PACF (MAXLAG, AC, PAC)

! Print results

CALL WRRRL (' ', PAC, RLABEL, CLABEL, FMT= '(F8.3)')

!

END

Output

 

Lag PACF

1 0.806

2 -0.635

3 0.078

4 -0.059

5 -0.001

6 0.172

7 0.109

8 0.110

9 0.079

10 0.079

11 0.069

12 -0.038

13 0.081

14 0.033

15 -0.035

16 -0.131

17 -0.155

18 -0.119

19 -0.016

20 -0.004

 

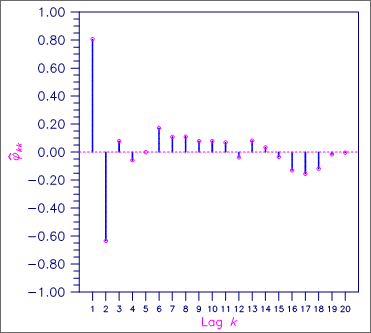
Figure 1,  Sample Partial Autocorrelation Function