Conjugate Gradient Example 2:
In this example, two different preconditioners are used to find the solution of a sparse positive definite linear system which occurs in a finite difference solution of Laplace's equation on a regular 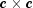 grid,
grid, 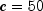 . The matrix is
. The matrix is 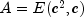 . For the first solution, Jacobi preconditioning with preconditioner
. For the first solution, Jacobi preconditioning with preconditioner 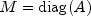 is used. The required iteration number and maximum absolute error are printed. Next, a more complicated preconditioning matrix, consisting of the symmetric tridiagonal part of A, is used. Again, the iteration number and the maximum absolute error are printed. The iteration number is substantially reduced.
is used. The required iteration number and maximum absolute error are printed. Next, a more complicated preconditioning matrix, consisting of the symmetric tridiagonal part of A, is used. Again, the iteration number and the maximum absolute error are printed. The iteration number is substantially reduced.
import com.imsl.math.*;
public class ConjugateGradientEx2 implements ConjugateGradient.Preconditioner {
private SparseMatrix A;
private SparseCholesky M;
public ConjugateGradientEx2(int n, int c) throws SparseCholesky.NotSPDException {
// Create matrix E(n,c), n>1, 1<c<n-1
// See Osterby and Zlatev(1982), pp. 7-8
A = new SparseMatrix(n, n);
for (int j = 0; j < n; j++) {
if (j-c >= 0) A.set(j, j-c, -1.0);
if (j-1 >= 0) A.set(j, j-1, -1.0);
A.set(j, j, 4.0);
if (j+1 < n) A.set(j, j+1, -1.0);
if (j+c < n) A.set(j, j+c, -1.0);
}
// Create and factor preconditioning matrix
SparseMatrix C = new SparseMatrix(n,n);
for (int j = 0; j < n; j++) {
if (j-1 >= 0) C.set(j, j-1, -1.0);
C.set(j, j, 4.0);
if (j+1 < n) C.set(j, j+1, -1.0);
}
M = new SparseCholesky(C);
M.factorSymbolically();
M.factorNumerically();
}
public void amultp(double[] p, double[] z) {
double w[] = A.multiply(p);
System.arraycopy(w, 0, z, 0, w.length);
}
public void preconditioner(double[] r, double[] z) {
try {
double w[] = M.solve(r);
System.arraycopy(w, 0, z, 0, w.length);
} catch (SparseCholesky.NotSPDException e) {
// No danger of NotSPDException because the system is only
// solved here for given Cholesky factor. This exception
// would have been thrown in the constructor already.
}
}
public static void main(String args[]) throws Exception {
int n = 2500;
int c = 50;
ConjugateGradientEx2 atp = new ConjugateGradientEx2(n, c);
// Set a predetermined answer and diagonal
double[] expected = new double[n];
double[] diagonal = new double[n];
for (int i = 0; i < n; i++) {
expected[i] = (double) (i % 5);
diagonal[i] = 4.0;
}
// Get right-hand side
double[] b = new double[n];
atp.amultp(expected, b);
// Solve system with Jacobi preconditioning
ConjugateGradient cgJacobi = new ConjugateGradient(n, atp);
cgJacobi.setJacobi(diagonal);
double solution[] = cgJacobi.solve(b);
// Compute inf-norm of computed solution - exact solution, print results
double norm = 0.0;
for (int i = 0; i < n; i++) {
norm = Math.max(norm, Math.abs(solution[i] - expected[i]));
}
System.out.println("Jacobi preconditioning");
System.out.println("Iterations= " + cgJacobi.getIterations()
+", norm= "+ norm);
System.out.println();
/*
* Solve the same system, with Cholesky preconditioner
*/
ConjugateGradient cgCholesky = new ConjugateGradient(n, atp);
solution = cgCholesky.solve(b);
norm = 0.0;
for (int i = 0; i < n; i++) {
norm = Math.max(norm, Math.abs(solution[i] - expected[i]));
}
System.out.println("More general preconditioning");
System.out.println("Iterations= "+cgCholesky.getIterations() +
", norm= "+ norm);
}
}
Output
Jacobi preconditioning
Iterations= 187, norm= 4.463440728130763E-10
More general preconditioning
Iterations= 127, norm= 5.137250624898115E-10
Link to Java source.