Example: Poisson Model.

In this example, the following data illustrate the Poisson model when all types of interval data are present. The example also illustrates the use of classification variables and the detection of potentially infinite estimates (which turn out here to be finite). These potential estimates lead to the two iteration summaries. The input data is
ilt irt icen Class 1 Class 2
0 5 0 1 0
9 4 3 0 0
0 4 1 0 0
9 0 2 1 1
0 1 0 0 1

A linear model 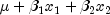\mu + \beta_1 x_1 + \beta_2 x_2 is fit where 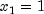x_1 = 1 if the Class 1 variable is 0, 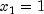x_1 = 1, otherwise, and the 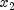x_2 variable is similarly defined 

import java.io.*;
import com.imsl.stat.*;
import com.imsl.math.*; 

public class CategoricalGenLinModelEx2 {  
    public static void main(String argv[]) throws Exception { 

        // Set up a PrintMatrix object for later use.
        PrintMatrixFormat mf;
        PrintMatrix p;
        p = new PrintMatrix();
        mf = new PrintMatrixFormat();
        mf.setNoRowLabels();
        mf.setNoColumnLabels();

        double[][] x  = {
            {0.0, 5.0, 0.0, 1.0, 0.0},
            {9.0, 4.0, 3.0, 0.0, 0.0},
            {0.0, 4.0, 1.0, 0.0, 0.0},
            {9.0, 0.0, 2.0, 1.0, 1.0},
            {0.0, 1.0, 0.0, 0.0, 1.0},
       };
        CategoricalGenLinModel CATGLM;
        CATGLM = new CategoricalGenLinModel(x,
                 CategoricalGenLinModel.MODEL0);
        CATGLM.setUpperEndpointColumn(0);
        CATGLM.setLowerEndpointColumn(1);
        CATGLM.setOptionalDistributionParameterColumn(1);
        CATGLM.setCensorColumn(2);
        CATGLM.setInfiniteEstimateMethod(0);
        CATGLM.setModelIntercept(1);
        int[] indcl = {3, 4};
        CATGLM.setClassificationVariableColumn(indcl);
        int[] nvef = {1, 1};
        int[] indef  = {3, 4};
        CATGLM.setEffects(indef, nvef);
        CATGLM.setUpperBound(4);


        p.setTitle("Coefficient Statistics");
        p.print(CATGLM.solve());
        System.out.println("Log likelihood " +
        CATGLM.getOptimizedCriterion());
        p.setTitle("Asymptotic Coefficient Covariance");
        p.setMatrixType(1);
        p.print(CATGLM.getCovarianceMatrix());
        p.setMatrixType(0);
        p.setTitle("Case Analysis");
        p.print(CATGLM.getCaseAnalysis());
        p.setTitle("Last Coefficient Update");
        p.print(CATGLM.getLastParameterUpdates());
        p.setTitle("Covariate Means");
        p.print(CATGLM.getDesignVariableMeans());
        p.setTitle("Distinct Values For Each Class Variable");
        p.print(CATGLM.getClassificationVariableValues());
        System.out.println("Number of Missing Values " +
           CATGLM.getNRowsMissing());
   }
}

Output

     Coefficient Statistics
     0       1      2       3    
0  -0.549  1.171  -0.469  0.64   
1   0.549  0.61    0.9    0.368  
2   0.549  1.083   0.507  0.612  

Log likelihood -3.1146384925784414
Asymptotic Coefficient Covariance
     0       1       2     
0   1.372  -0.372  -1.172  
1           0.372   0.172  
2                   1.172  

             Case Analysis
     0      1       2      3      4     
0  5      -0      2.236  1      -0      
1  6.925  -0.412  2.108  0.764  -0.196  
2  6.925   0.412  1.173  0.236   0.351  
3  0       0      0      0       ?      
4  1      -0      1      1      -0      

Last Coefficient Update
   0   
0  -0  
1   0  
2   0  

Covariate Means
    0   
0  0.6  
1  0.6  
2  0    

Distinct Values For Each Class Variable
   0  
0  0  
1  1  
2  0  
3  1  

Number of Missing Values 0
Link to Java source.