Example 6: Usage With Class MinUnconMultiVar
The minimum of 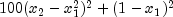 is found using
is found using MinUnconMultiVar
. NumericalDerivatives
is used to compute the numerical gradients.
import com.imsl.math.*;
import java.text.*;
public class NumericalDerivativesEx6 {
static int m = 1, n = 2;
static double fcnEvaluation(double[] x) {
return 100.*((x[1] - x[0] * x[0]) * (x[1] - x[0] * x[0])) +
(1. - x[0]) * (1. - x[0]);
}
static class MyFunction implements MinUnconMultiVar.Gradient {
public double f(double[] x) {
return fcnEvaluation(x);
}
public void gradient(double[] x, double[] gp) {
NumericalDerivatives.Function fcn = new NumericalDerivatives.Function() {
public double[] f(int varIndex, double[] y) {
double[] tmp = new double[m];
tmp[0] = fcnEvaluation(y);
return tmp;
}
};
NumericalDerivatives nderv = new NumericalDerivatives(fcn);
double[][] jacobian = nderv.evaluateJ(x);
gp[0] = jacobian[0][0];
gp[1] = jacobian[0][1];
}
}
public static void main(String args[]) throws Exception {
MinUnconMultiVar solver = new MinUnconMultiVar(n);
solver.setGuess(new double[]{-1.2, 1.0});
double x[] = solver.computeMin(new MyFunction());
System.out.println("Minimum point is (" + x [0] + ", " + x[1] + ")");
}
}
Output
Minimum point is (0.9999986118580241, 0.9999972746481575)
Link to Java source.