Example

The data for this example comes from the function 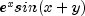e^x sin(x + y) on the rectangle [0, 3] x [0, 5]. This function is first sampled on a 50 x 25 grid. Next, an attempt to recover it by using tensor-product cubic splines is performed. The values of the function 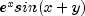e^x sin(x + y) are printed on a 2 x 2 grid and compared with the values of the tensor-product spline least-squares fit. 
import java.text.*;
import com.imsl.math.*;

public class Spline2DLeastSquaresEx1 {
    
    private static double F(double x, double y) {
        return (Math.exp(x) * Math.sin(x + y));
    }
    
    public static void main(String args[]) {
        int nxData = 50, nyData = 25, outData = 2;
        double[] xData = new double[nxData];
        double[] yData = new double[nyData];
        double[][] fData = new double[nxData][nyData];
        double x, y, z;
        
        // Set up grid
        for (int i = 0; i < nxData; i++) {
            xData[i] = 3.*(double) i / ((double) (nxData - 1));
        }
        for (int i = 0; i < nyData; i++) {
            yData[i] = 5.*(double) i / ((double) (nyData - 1));
        }
        
        // Compute function values on grid
        for (int i = 0; i < nxData; i++) {
            for (int j = 0; j < nyData; j++) {
                fData[i][j] = F(xData[i], yData[j]);
            }
        }
        
        // Compute tensor-product approximant
        Spline2DLeastSquares spline =
                new Spline2DLeastSquares(xData, yData, fData, 5, 7);
        
        spline.compute();
        x = spline.getErrorSumOfSquares();
        
        NumberFormat nf = NumberFormat.getInstance();
        nf.setMaximumFractionDigits(4);
        nf.setMinimumFractionDigits(4);
        
        // Print results
        System.out.println("The error sum of squares is " +
                nf.format(x) + "\n");
        
        double[][] output = new double[outData*outData][5];
        for (int i = 0, idx = 0; i < outData; i++) {
            x = (double) i / (double) (outData);
            for (int j = 0; j < outData; j++) {
                y = (double) j / (double) (outData);
                z = spline.value(x, y);
                output[idx][0] = x;
                output[idx][1] = y;
                output[idx][2] = F(x,y);
                output[idx][3] = z;
                output[idx][4] = Math.abs(F(x,y)-z);
                idx++;
            }
        }
        
        String[] labels = {"x", "y", "F(x, y)", "Fitted Values", "Error"};
        PrintMatrixFormat pmf = new PrintMatrixFormat();
        pmf.setNumberFormat(nf);
        pmf.setColumnLabels(labels);
        new PrintMatrix().print(pmf, output);
    }
}

Output

The error sum of squares is 3.7532

     x       y     F(x, y)  Fitted Values  Error   
0  0.0000  0.0000  0.0000      -0.0204     0.0204  
1  0.0000  0.5000  0.4794       0.5002     0.0208  
2  0.5000  0.0000  0.7904       0.8158     0.0253  
3  0.5000  0.5000  1.3874       1.3842     0.0031
Link to Java source.