Example 3: Accumulation Of A Component

This example uses the same data as in the One-Sided Differences example. An alternate examination of the function 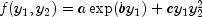f(y_1 ,y_2 ) = a\exp (by_1 ) + cy_1 y_2^2 shows that the first term on the right-hand side need be evaluated just when computing the first partial. The additive term 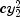cy_2^2 occurs when computing the partial with respect to 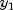y_1. Also the first term does not depend on the second variable. Thus the first term can be left out of the function evaluation when computing the partial with respect to 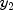y_2, potentially avoiding cancellation errors. The input values of array options allow NumericalDerivatives to use these facts and obtain greater accuracy using a minimum number of computations of the exponential function. 
import com.imsl.math.*;
import java.text.*;

public class NumericalDerivativesEx3 {    
    static int m = 1, n = 2;
    static double a, b, c, f2 = 0.0;
    
    
    public static void main(String args[]) {
        int[] options = new int[n];
        double u;
        double[] y = new double[n];
        double[] valueF = new double[m];
        double[] scale = new double[n];
        double[][] actual = new double[m][n];
        double[] re = new double[2];
    
        // Define data and point of evaluation:
        a = 2.5e6;
        b = 3.4e0;
        c = 4.5e0;
        y[0] = 2.1e0;
        y[1] = 3.2e0;
        
        // Precision, for measuring errors
        u = Math.sqrt(2.220446049250313e-016);
        
        // Set scaling:
        scale[0] = 1.e0;
        // Increase scale to account for large value of a.
        scale[1] = 8.e3;
        
        // Compute true values of partials.
        actual[0][0] = a * b * Math.exp(b * y[0]) + c * y[1] * y[1];
        actual[0][1] = 2 * c * y[0] * y[1];
        
        options[0] = NumericalDerivatives.ACCUMULATE;
        options[1] = NumericalDerivatives.ONE_SIDED;
        
        valueF[0] = a * Math.exp(b * y[0]);
        scale[1] = 1.e0;
        
        NumericalDerivatives.Jacobian fcn = new NumericalDerivatives.Jacobian() {
            public double[] f(int varIndex, double[] y) {
                double[] tmp = new double[m];
                
                if (varIndex != 2) {
                    tmp[0] = a * Math.exp(b * y[0]);
                } else {
                    // This is the function value for the partial wrt y_2.
                    tmp[0] = c * y[0] * y[1] * y[1];
                }
                
                return tmp;
            }
            
            public double[][] jacobian(double[] y) {
                double[][] tmp = new double[m][n];
                
                // Start with part of the derivative that is known.
                tmp[0][0] = c * y[1] * y[1];
                
                return tmp;
            }
        };
        
        NumericalDerivatives derv = new NumericalDerivatives(fcn);
        derv.setDifferencingMethods(options);
        derv.setScalingFactors(scale);
        derv.setInitialF(valueF);
        double[][] jacobian = derv.evaluateJ(y);
        
        NumberFormat nf = NumberFormat.getInstance();
        nf.setMaximumFractionDigits(2);
        nf.setMinimumFractionDigits(2);
        
        PrintMatrixFormat pmf = new PrintMatrixFormat();
        pmf.setNumberFormat(nf);
        new PrintMatrix("Numerical gradient:").print(pmf, jacobian);
        new PrintMatrix("Analytic gradient:").print(pmf, actual);
        
        jacobian[0][0] = (jacobian[0][0] - actual[0][0]) / actual[0][0];
        jacobian[0][1] = (jacobian[0][1] - actual[0][1]) / actual[0][1];
        re[0] = jacobian[0][0];
        re[1] = jacobian[0][1];
        
        System.out.println("Relative accuracy:");
        System.out.println("df/dy_1       df/dy_2");
        System.out.printf(" %.2fu        %.2fu\n", re[0]/u, re[1]/u);
        System.out.printf("(%.3e)  (%.3e)\n", re[0], re[1]);
    }
}

Output

     Numerical gradient:
           0            1    
0  10,722,141,710.08  60.48  

     Analytic gradient:
           0            1    
0  10,722,141,353.42  60.48  

Relative accuracy:
df/dy_1       df/dy_2
 2.23u        -0.51u
(3.326e-08)  (-7.569e-09)
Link to Java source.