LU Factorization of a Comples Sparse Matrix

Example: LU Factorization of a Complex Sparse Matrix

The LU Factorization of the sparse complex $6 \times 6$ matrix

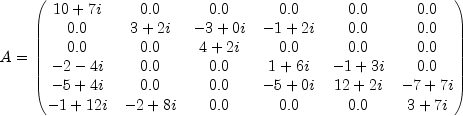
$A=\begin{pmatrix} 10+7i & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 3+2i & -3+0i & -1+2i & 0.0 & 0.0 \\ 0.0 & 0.0 & 4+2i & 0.0 & 0.0 & 0.0 \\ -2-4i & 0.0 & 0.0 & 1+6i & -1+3i & 0.0 \\ -5+4i & 0.0 & 0.0 & -5+0i & 12+2i & -7+7i \\ -1+12i & -2+8i & 0.0 & 0.0 & 0.0 & 3+7i \end{pmatrix}$ is computed. The sparse coordinate form for A is given by row, column, value triplets:

row	column	value
0	0	10+7i
1	1	3+2i
1	2	-3+0i
1	3	-1+2i
2	2	4+2i
3	0	-2-4i
3	3	1+6i
3	4	-1+3i
4	0	-5+4i
4	3	-5+0i
4	4	12+2i
4	5	-7+7i
5	0	-1+12i
5	1	-2+8i
5	5	3+7i

Let

so that $b_1:=Ax = {(3+17i, -19+5i, 6+18i, -38+32i, -63+49i, -57+83i)}^T$ and $b_2:=A^Hx = {(54-112i, 46-58i, 12, 5-51i, 78+34i, 60-94i)}^T\,.$

The LU factorization of is used to solve the complex sparse linear systems and with iterative refinement. The reciprocal pivot growth factor and the reciprocal condition number are also computed.


import com.imsl.math.*;

public class ComplexSuperLUEx1 {

    public static void main(String args[]) throws Exception {
        int m;
        ComplexSuperLU ComplexSparseLU;
        double conditionNumber, recip_pivot_growth;
        Complex[] sol = null;
        double Ferr, Berr;

        Complex[] b1 = {
            new Complex(3.0, 17.0), new Complex(-19.0, 5.0),
            new Complex(6.0, 18.0), new Complex(-38.0, 32.0),
            new Complex(-63.0, 49.0), new Complex(-57.0, 83.0)
        };

        Complex[] b2 = {
            new Complex(54.0, -112.0), new Complex(46.0, -58.0),
            new Complex(12.0, 0.0), new Complex(5.0, -51.0),
            new Complex(78.0, 34.0), new Complex(60.0, -94.0)
        };

        // Initialize input matrix A.
        m = 6;
        ComplexSparseMatrix a = new ComplexSparseMatrix(m, m);

        a.set(0, 0, new Complex(10.0, 7.0));
        a.set(1, 1, new Complex(3.0, 2.0));
        a.set(1, 2, new Complex(-3.0, 0.0));
        a.set(1, 3, new Complex(-1.0, 2.0));
        a.set(2, 2, new Complex(4.0, 2.0));
        a.set(3, 0, new Complex(-2.0, -4.0));
        a.set(3, 3, new Complex(1.0, 6.0));
        a.set(3, 4, new Complex(-1.0, 3.0));
        a.set(4, 0, new Complex(-5.0, 4.0));
        a.set(4, 3, new Complex(-5.0, 0.0));
        a.set(4, 4, new Complex(12.0, 2.0));
        a.set(4, 5, new Complex(-7.0, 7.0));
        a.set(5, 0, new Complex(-1.0, 12.0));
        a.set(5, 1, new Complex(-2.0, 8.0));
        a.set(5, 5, new Complex(3.0, 7.0));

        // Compute the sparse LU factorization of a
        ComplexSparseLU = new ComplexSuperLU(a);

        ComplexSparseLU.setEquilibrate(false);
        ComplexSparseLU.setColumnPermutationMethod(
                ComplexSuperLU.NATURAL_ORDERING);
        ComplexSparseLU.setPivotGrowth(true);

        // Set option of iterative refinement
        ComplexSparseLU.setIterativeRefinement(true);

        // Solve sparse system A*x = b1
        System.out.println();
        System.out.println("Solve sparse System Ax=b1");
        System.out.println("=========================");
        System.out.println();

        sol = ComplexSparseLU.solve(b1);
        new PrintMatrix("Solution").print(sol);

        Ferr = ComplexSparseLU.getForwardErrorBound();
        Berr = ComplexSparseLU.getRelativeBackwardError();

        System.out.println();
        System.out.println("Forward error bound: " + Ferr);
        System.out.println("Relative backward error: " + Berr);
        System.out.println();
        System.out.println();

        // Solve sparse system A^H*x = b2
        System.out.println();
        System.out.println("Solve sparse System A^Hx=b2");
        System.out.println("===========================");
        System.out.println();

        sol = ComplexSparseLU.solveConjugateTranspose(b2);
        new PrintMatrix("Solution").print(sol);

        Ferr = ComplexSparseLU.getForwardErrorBound();
        Berr = ComplexSparseLU.getRelativeBackwardError();

        System.out.println();
        System.out.println("Forward error bound: " + Ferr);
        System.out.println("Relative backward error: " + Berr);
        System.out.println();
        System.out.println();

        // Compute reciprocal pivot growth factor and condition number
        recip_pivot_growth
                = ComplexSparseLU.getReciprocalPivotGrowthFactor();
        conditionNumber = ComplexSparseLU.getConditionNumber();

        System.out.println("Pivot growth factor and condition number");
        System.out.println("========================================");
        System.out.println();

        System.out.println("Reciprocal pivot growth factor: "
                + recip_pivot_growth);
        System.out.println("Reciprocal condition number: "
                + conditionNumber);
        System.out.println();
    }
}

Output


Solve sparse System Ax=b1
=========================

Solution
    0    
0  1+1i  
1  2+2i  
2  3+3i  
3  4+4i  
4  5+5i  
5  6+6i  


Forward error bound: 2.8393330592805326E-15
Relative backward error: 1.708035422500241E-16



Solve sparse System A^Hx=b2
===========================

Solution
    0    
0  1+1i  
1  2+2i  
2  3+3i  
3  4+4i  
4  5+5i  
5  6+6i  


Forward error bound: 8.54834098797111E-15
Relative backward error: 1.0297720808117394E-16


Pivot growth factor and condition number
========================================

Reciprocal pivot growth factor: 0.7993827160493826
Reciprocal condition number: 0.07006544790967506

Link to Java source.