Package com.imsl.finance

Class Bond

java.lang.Object
com.imsl.finance.Bond
public class Bond extends Object
Collection of bond functions.

Definitions

rate is an annualized rate of return based on the par value of the bills.

yield is an annualized rate based on the purchase price and reflects the actual yield to maturity.

coupons are interest payments on a bond.

redemption is the amount a bond pays at maturity.

frequency is the number of times a year that a bond makes interest payments.

basis is the method used to calculate dates. For example, sometimes computations are done assuming 360 days in a year.

issue is the day a bond is first sold.

settlement is the day a purchaser acquires a bond.

maturity is the day a bond's principal is repaid.

Discount Bonds

Discount bonds, also called zero-coupon bonds, do not pay interest during the life of the security, instead they sell at a discount to their value at maturity. The discount bond methods all have settlement, maturity, basis, and redemption as arguments. In the following list these common arguments are omitted. A related method is accrintm, which returns the interest that has accumulated on the discount bond.

Treasury Bills

US Treasury bills are a special case of discount bonds. The basis is fixed for treasury bills and the redemption value is assumed to be $100. So these functions have only settlement and maturity as common arguments.

Interest-Paying Bonds

Most bonds pay interest periodically. The interest-paying bond methods all have settlement, maturity, basis, and frequency as arguments. Again suppressing the common arguments,
  • price = price(rate, yield, redemption)
  • yield = yield(rate, price, redemption)
  • redemption = received(price, rate)
A related method is accrint, which returns the interest that has accumulated at settlement from the previous coupon date.

Interest-Paying Bonds with Odd Coupon Periods

An odd coupon period is one that is either shorter or longer than the regular coupon period. Odd coupon periods typically occur in the first or the last payment period. The yield and price functions accept two additional arguments in order to make the proper adjustments for odd coupon periods: issueDate and firstCouponDate or lastCouponDate.

Coupon days

In this diagram, the settlement date is shown as a hollow circle and the adjacent coupon dates are shown as filled circles.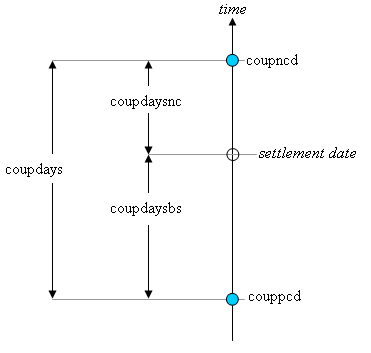

  • coupppcd is the coupon date immediately prior to the settlement date.
  • coupncd is the coupon date immediately after the settlement date.
  • coupdaysbs is the number of days from the immediately prior coupon date to the settlement date.
  • coupdaysnc is the number of days from the settlement date to the next coupon date.
  • coupdays is the number of days between these two coupon dates.
A related method is coupnum, which returns the number of coupons payable between settlement and maturity.

Another related method is yearfrac, which returns the fraction of the year between two days.

Duration

Duration is used to measure the sensitivity of a bond to changes in interest rates. Convexity is a measure of the sensitivity of duration.

  • Field Details

    • ANNUAL

      public static final int ANNUAL
      Coupon payments are made annually.
      See Also:

    • SEMIANNUAL

      public static final int SEMIANNUAL
      Coupon payments are made semiannually (twice per year).
      See Also:

    • QUARTERLY

      public static final int QUARTERLY
      Coupon payments are made quarterly.
      See Also:

    • BIMONTHLY

      public static final int BIMONTHLY
      Coupon payments are made bimonthly (6 times per year).
      See Also:

    • MONTHLY

      public static final int MONTHLY
      Coupon payments are made monthly.
      See Also:

  • Method Details

    • accrint

      public static double accrint(GregorianCalendar issue, GregorianCalendar firstCoupon, GregorianCalendar settlement, double rate, double par, int frequency, DayCountBasis basis)
      Returns the interest which has accrued on a security that pays interest periodically. In the equation below, Ai represents the number of days which have accrued for the ith quasi-coupon period within the odd period. The quasi-coupon periods are periods obtained by extending the series of equal payment periods to before or after the actual payment periods. NC represents the number of quasi-coupon periods within the odd period, rounded to the next highest integer. NLi represents the length of the normal ith quasi-coupon period within the odd period. NLi is expressed in days. Function accrint can be found by solving the following:

      $${\it par} \left({{{\it rate} \over {\it frequency}} {\sum\limits_{i = 1}^{\it NC} {{{{A_i } \over {{\it NL}_i }}}} }} \right)$$

      Parameters:
      issue - a GregorianCalendar, the issue date of the security
      firstCoupon - a GregorianCalendar, the date of the first interest payment
      settlement - a GregorianCalendar, the settlement date of the security
      rate - a double specifying the annual coupon rate
      par - a double specifying the par value
      frequency - an int specifying the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object containing the type of day count basis to use. See DayCountBasis.
      Returns:
      a double, the accrued interest
      See Also:

    • accrintm

      public static double accrintm(GregorianCalendar issue, GregorianCalendar maturity, double rate, double par, DayCountBasis basis)
      Returns the interest which has accrued on a security that pays interest at maturity.

      $$= {\it par} \times {\it rate} \times {\frac{A}{D}}$$

      In the above equation, \(A\) represents the number of days starting at issue date to maturity date and \(D\) represents the annual basis.
      Parameters:
      issue - a GregorianCalendar issue date of the security
      maturity - a GregorianCalendar date of the security's maturity
      rate - a double which specifies the security's annual coupon rate
      par - a double which specifies the security's par value
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the accrued interest
      See Also:

    • amordegrc

      public static double amordegrc(double cost, GregorianCalendar issue, GregorianCalendar firstPeriod, double salvage, int period, double rate, DayCountBasis basis)
      Returns the depreciation for each accounting period. This method is similar to amorlinc. However, in this method a depreciation coefficient based on the asset life is applied during the evaluation of the function.
      Parameters:
      cost - a double which specifies the cost of the asset
      issue - a GregorianCalendar issue date of the asset
      firstPeriod - a GregorianCalendar date of the end of the first period
      salvage - a double which specifies the asset's salvage value at the end of the life of the asset
      period - an int which specifies the period
      rate - a double which specifies the rate of depreciation
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the depreciation
      See Also:

    • amorlinc

      public static double amorlinc(double cost, GregorianCalendar issue, GregorianCalendar firstPeriod, double salvage, int period, double rate, DayCountBasis basis)
      Returns the depreciation for each accounting period. This method is similar to amordegrc, except that amordegrc has a depreciation coefficient that is applied during the evaluation that is based on the asset life.
      Parameters:
      cost - a double which specifies the cost of the asset
      issue - a GregorianCalendar issue date of the asset
      firstPeriod - a GregorianCalendar date of the end of the first period
      salvage - a double which specifies the asset's salvage value at the end of the life of the asset
      period - an int which specifies the period
      rate - a double which specifies the rate of depreciation
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the depreciation
      See Also:

    • coupdays

      public static double coupdays(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)
      Returns the number of days in the coupon period containing the settlement date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the number of days in the coupon period that contains the settlement date
      See Also:

    • coupdaysbs

      public static int coupdaysbs(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)
      Returns the number of days starting with the beginning of the coupon period and ending with the settlement date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      an int which specifies the number of days from the beginning of the coupon period to the settlement date
      See Also:

    • coupdaysnc

      public static int coupdaysnc(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)
      Returns the number of days starting with the settlement date and ending with the next coupon date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      an int which specifies the number of days from the settlement date to the next coupon date
      See Also:

    • couppcd

      public static GregorianCalendar couppcd(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)
      Returns the coupon date which immediately precedes the settlement date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis
      Returns:
      a GregorianCalendar which specifies the previous coupon date before the settlement date
      See Also:

    • coupncd

      public static GregorianCalendar coupncd(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)
      Returns the first coupon date which follows the settlement date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis
      Returns:
      a GregorianCalendar which specifies the next coupon date after the settlement date
      See Also:

    • coupnum

      public static int coupnum(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)
      Returns the number of coupons payable between the settlement date and the maturity date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      an int which specifies the number of coupons payable between the settlement date and maturity date
      See Also:

    • disc

      public static double disc(GregorianCalendar settlement, GregorianCalendar maturity, double price, double redemption, DayCountBasis basis)
      Returns the implied interest rate of a discount bond. The discount rate is the interest rate implied when a security is sold for less than its value at maturity in lieu of interest payments. It is computed using the following:

      $${{{{\it redemption} - {\it price}} \over {\it price}}} \times {{B \over {\it DSM}}}$$

      In the equation above, \(B\) represents the number of days in a year based on the annual basis and \({\it DSM}\) represents the number of days starting with the settlement date and ending with the maturity date.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      price - a double which specifies the security's price per $100 face value
      redemption - a double which specifies the security's redemption value per $100 face value
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the discount rate for a security
      See Also:

    • duration

      public static double duration(GregorianCalendar settlement, GregorianCalendar maturity, double coupon, double yield, int frequency, DayCountBasis basis)
      Returns the Macaulay duration of a security where the security has periodic interest payments. The Macaulay duration is the weighted-average time to the payments, where the weights are the present value of the payments. It is computed using the following:

      $$\left({{{{{\left({N - 1 + {{\it DSC}\over E}}\right)\times 100}\over {\left({1 + {{\it yield}\over {\it freq}}} \right)^{\left({N - 1 + {{\it DSC}\over E}}\right)}}} + \sum\limits_{k = 1}^N {}\left({\left({{{100\times {\it coupon}}\over {{\it freq}\times \left({1 + {{\it yield}\over {\it freq}}}\right)^{\left({k - 1 + {{\it DSC}\over E}}\right)}}}}\right)\times\left({k - 1 + {{\it DSC}\over E}} \right)}\right)}\over{{{100} \over {\left({1 + {{\it yield}\over {\it freq}}}\right)^{\left(N - 1 + {{\it DSC}\over E}\right)}}} + \sum \limits_{k = 1}^N {}\left({{{100 \times {\it coupon}}\over {{\it freq} \times\left({1 + {{\it yield}\over {\it freq}}}\right)^{\left(k - 1 + {{ \it DSC}\over E}\right)}}}} \right)}}}\right)\times {1\over {\it freq}} $$

      In the equation above, \({\it DSC}\) represents the number of days starting with the settlement date and ending with the next coupon date. \(E\) represents the number of days within the coupon period. \(N\) represents the number of coupons payable from the settlement date to the maturity date. \({\it freq}\) represents the frequency of the coupon payments annually.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      coupon - a double which specifies the security's annual coupon rate
      yield - a double which specifies the security's annual yield
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the annual duration of a security with periodic interest payments
      See Also:

    • convexity

      public static double convexity(GregorianCalendar settlement, GregorianCalendar maturity, double coupon, double yield, int frequency, DayCountBasis basis)
      Returns the convexity for a security. Convexity is the sensitivity of the duration of a security to changes in yield. It is computed using the following:

      $${{{1 \over {\left( {q \times {\it frequency}} \right)^2 }}\left\{ {\sum\limits_{t = 1}^n {t\left( {t + 1} \right)} \left( {{{\it coupon} \over {\it frequency}}} \right)q^{ - t} + n\left( {n + 1} \right)q^{ - n} } \right\}} \over {\left( {\sum\limits_{t = 1}^n {\left( {{{\it coupon} \over {\it frequency}}} \right)q^{ - t} } + q^{ - n} } \right)}}$$

      where n is calculated from coupnum, and \(q = 1 + {{\it yield} \over {\it frequency}}$$.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      coupon - a double which specifies the security's annual coupon rate
      yield - a double which specifies the security's annual yield
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the convexity for a security
      See Also:

    • intrate

      public static double intrate(GregorianCalendar settlement, GregorianCalendar maturity, double investment, double redemption, DayCountBasis basis)
      Returns the interest rate of a fully invested security. It is computed using the following:

      $${{{\it redemption} - {\it investment}} \over {\it investment}} \times {{B \over {\it DSM}}}$$

      In the equation above, \(B\) represents the number of days in a year based on the annual basis, and \({\it DSM}\) represents the number of days in the period starting with the settlement date and ending with the maturity date.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      investment - a double which specifies the amount invested
      redemption - a double which specifies the amount to be received at maturity
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the interest rate for a fully invested security
      See Also:

    • mduration

      public static double mduration(GregorianCalendar settlement, GregorianCalendar maturity, double coupon, double yield, int frequency, DayCountBasis basis)
      Returns the modified Macaulay duration for a security with an assumed par value of $100. It is computed using the following:

      $${\it duration} \over {1 + {{\it yield} \over {\it frequency}}}$$

      where \({\it duration}\) is calculated from mduration.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      coupon - a double which specifies the security's annual coupon rate
      yield - a double which specifies the security's annual yield
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the modified Macaulay duration for a security with an assumed par value of $100
      See Also:

    • price

      public static double price(GregorianCalendar settlement, GregorianCalendar maturity, double rate, double yield, double redemption, int frequency, DayCountBasis basis)
      Returns the price, per $100 face value, of a security that pays periodic interest. It is computed using the following:

      $${{{\it redemption} \over {\left( {1 + {{\it yield} \over {\it frequency}}} \right)^{\left( {N - 1 + {{\it DSC} \over E}} \right)} }}} + {\sum\limits_{k = 1}^N {{{100 \times {{\it rate} \over {\it frequency}}} \over {\left( {1 + {{\it yield} \over {\it frequency}}} \right)^{\left( {k - 1 + {{\it DSC} \over E}} \right)} }}} } - \left( {100 \times {{\it rate} \over {\it frequency}} \times {A \over E}} \right)$$

      In the above equation, \({\it DSC}\) represents the number of days in the period starting with the settlement date and ending with the next coupon date. \(E\) represents the number of days within the coupon period. \(N\) represents the number of coupons payable in the timeframe from the settlement date to the redemption date. \(A\) represents the number of days in the timeframe starting with the beginning of coupon period and ending with the settlement date.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      rate - a double which specifies the annual coupon rate
      yield - a double which specifies the annual yield
      redemption - a double which specifies the redemption value per $100 face value
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the price per $100 face value of a security that pays periodic interest
      See Also:

    • pricedisc

      public static double pricedisc(GregorianCalendar settlement, GregorianCalendar maturity, double rate, double redemption, DayCountBasis basis)
      Returns the price of a discount bond given the discount rate. It is computed using the following:

      $${\it redemption} - {\it rate} \times {\it redemption} \times {{\it DSM} \over B}$$

      In the equation above, \({\it DSM}\) represents the number of days starting at the settlement date and ending with the maturity date. \(B\) represents the number of days in a year based on the annual basis.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      rate - a double which specifies the discount rate
      redemption - a double which specifies the redemption value per $100 face value
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the price per $100 face value of a discounted security
      See Also:

    • priceyield

      public static double priceyield(GregorianCalendar settlement, GregorianCalendar maturity, double yield, double redemption, DayCountBasis basis)
      Returns the price of a discount bond given the yield. It is computed using the following:

      $${{\it redemption} \over {1 + \left( {{{\it DSM} \over B}} \right) {\it yield}}}$$

      In the equation above, \({\it DSM}\) represents the number of days starting at the settlement date and ending with the maturity date. \(B\) represents the number of days in a year based on the annual basis.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      yield - a double which specifies the security's yield
      redemption - a double which specifies the security's redemption value per $100 face value
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis
      Returns:
      a double which specifies the price per $100 face value of a discounted security
      See Also:

    • pricemat

      public static double pricemat(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar issue, double rate, double yield, DayCountBasis basis)
      Returns the price, per $100 face value, of a discount bond. It is computed using the following:

      $${{{100 + \left( {{{\it DIM} \over B} \times rate \times 100} \right)} \over {1 + \left( {{{\it DSM} \over B} \times {\it yield}} \right)}}} - {{A \over B} \times {\it rate} \times 100}$$

      In the equation above, \(B\) represents the number of days in a year based on the annual basis. \({\it DSM}\) represents the number of days in the period starting with the settlement date and ending with the maturity date. \({\it DIM}\) represents the number of days in the period starting with the issue date and ending with the maturity date. \(A\) represents the number of days in the period starting with the issue date and ending with the settlement date.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      issue - a GregorianCalendar issue date of the security
      rate - a double which specifies the security's interest rate at issue date
      yield - a double which specifies the security's annual yield
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the price per $100 face value of a security that pays interest at maturity
      See Also:

    • received

      public static double received(GregorianCalendar settlement, GregorianCalendar maturity, double investment, double rate, DayCountBasis basis)
      Returns the amount one receives when a fully invested security reaches the maturity date. It is computed using the following:

      $${{\it investment} \over {1 - \left( {{\it rate} \times {{\it DIM} \over B}} \right)}}$$

      In the equation above, \(B\) represents the number of days in a year based on the annual basis, and \({\it DIM}\) represents the number of days in the period starting with the issue date and ending with the maturity date.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      investment - a double which specifies the amount invested in the security
      rate - a double which specifies the security's rate at issue date
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the amount received at maturity for a fully invested security
      See Also:

    • tbilleq

      public static double tbilleq(GregorianCalendar settlement, GregorianCalendar maturity, double rate)
      Returns the bond-equivalent yield of a Treasury bill. It is computed using the following:

      If \(DSM \lt =182\)
      $$ {{365 \times {\it rate}} \over {360 - {\it rate} \times {\it DSM}}}$$

      otherwise,

      $${{ - {{\it DSM} \over {365}} + \sqrt {\left( {{{\it DSM} \over {365}}} \right)^2 - \left( {2 \times {{\it DSM} \over {365}} - 1} \right) \times {{{\it rate} \times {\it DSM}} \over {{\it rate} \times {\it DSM} - {360}}}} } \over {{{\it DSM} \over {365}} - 0.5}}$$

      In the above equation, \({\it DSM}\) represents the number of days starting at settlement date to maturity date.
      Parameters:
      settlement - a GregorianCalendar settlement date of the Treasury bill
      maturity - a GregorianCalendar maturity date of the Treasury bill. The maturity cannot be more than a year after the settlement.
      rate - a double which specifies the Treasury bill's discount rate at issue date. The discount rate is an annualized rate of return based on the par value of the bills. The discount rate is calculated on a 360-day basis (twelve 30-day months).
      Returns:
      a double which specifies the bond-equivalent yield for the Treasury bill. This is an annualized rate based on the purchase price of the bills and reflects the actual yield to maturity.
      See Also:

    • tbillprice

      public static double tbillprice(GregorianCalendar settlement, GregorianCalendar maturity, double rate)
      Returns the price, per $100 face value, of a Treasury bill. It is computed using the following:

      $$100 \left( {1 - {{{\it rate} \times {\it DSM}} \over {360}}} \right)$$

      In the equation above, \({\it DSM}\) represents the number of days in the period starting with the settlement date and ending with the maturity date (any maturity date that is more than one calendar year after the settlement date is excluded).
      Parameters:
      settlement - a GregorianCalendar settlement date of the Treasury bill
      maturity - a GregorianCalendar maturity date of the Treasury bill. The maturity cannot be more than a year after the settlement
      rate - a double which specifies the Treasury bill's discount rate at issue date. The discount rate is an annualized rate of return based on the par value of the bills. The discount rate is calculated on a 360-day basis (twelve 30-day months).
      Returns:
      a double which specifies the price per $100 face value for the Treasury bill
      See Also:

    • tbillyield

      public static double tbillyield(GregorianCalendar settlement, GregorianCalendar maturity, double price)
      Returns the yield of a Treasury bill. It is computed using the following:

      $${{{100 - {\it price}} \over {\it price}}} \times {{{360} \over {\it DSM}}}$$

      In the equation above, \({\it DSM}\) represents the number of days in the period starting with the settlement date and ending with the maturity date (any maturity date that is more than one calendar year after the settlement date is excluded).
      Parameters:
      settlement - a GregorianCalendar settlement date of the Treasury bill
      maturity - a GregorianCalendar maturity date of the Treasury bill. The maturity cannot be more than a year after the settlement.
      price - a double which specifies the Treasury bill's price per $100 face value
      Returns:
      a double which specifies the yield for the Treasury bill. This is an annualized rate based on the purchase price of the bills and reflects the actual yield to maturity.
      See Also:

    • yielddisc

      public static double yielddisc(GregorianCalendar settlement, GregorianCalendar maturity, double price, double redemption, DayCountBasis basis)
      Returns the annual yield of a discount bond. It is computed using the following:

      $${{{{\it redemption} - {\it price}} \over {\it price}}} \times {{B \over {\it DSM}}}$$

      In the equation above, \(B\) represents the number of days in a year based on the annual basis, and \({\it DSM}\) represents the number of days starting with the settlement date and ending with the maturity date.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      price - a double which specifies the security's price per $100 face value
      redemption - a double which specifies the security's redemption value per $100 face value
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the annual yield for a discounted security
      See Also:

    • yield

      public static double yield(GregorianCalendar settlement, GregorianCalendar maturity, double rate, double price, double redemption, int frequency, DayCountBasis basis)
      Returns the yield of a security that pays periodic interest. If there is one coupon period, use the following:

      $${{{\left( {{{\it redemption} \over {100}} + {{\it rate} \over {\it frequency}}} \right) - \left[ {{{\it price} \over {100}} + \left( {{A \over E} \times {{\it rate} \over {\it frequency}}} \right)} \right]} \over {{{\it price} \over {100}} + \left( {{A \over E} \times {{\it rate} \over {\it frequency}}} \right)}}} \times {{{{\it frequency} \times E} \over {\it DSR}}}$$

      In the equation above, \(DSR\) represents the number of days in the period starting with the settlement date and ending with the redemption date. \(E\) represents the number of days within the coupon period. \(A\) represents the number of days in the period starting with the beginning of coupon period and ending with the settlement date.

      If there is more than one coupon period, use the following:

      $${\it price} - {{\it redemption} \over {\left( {1 + {\it yield} \over {\it frequency}} \right)}^{N - 1 + {\it DSC} \over E}} - {\left( {\sum\limits_{k = 1}^N { {100 \times {{\it rate} \over {\it frequency}}} \over {\left( {1 + {\it yield} \over {\it frequency}} \right)}^{k - 1 + {\it DSC} \over E} }} \right) } + {100 \times {{\it rate} \over {\it frequency}} \times {A \over E} }$$

      In the equation above, \({\it DSC}\) represents the number of days in the period from the settlement to the next coupon date. \(E\) represents the number of days within the coupon period.\(N\) represents the number of coupons payable in the period starting with the settlement date and ending with the redemption date. \(A\) represents the number of days in the period starting with the beginning of the coupon period and ending with the settlement date.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      rate - a double which specifies the security's annual coupon rate
      price - a double which specifies the security's price per $100 face value
      redemption - a double which specifies the security's redemption value per $100 face value
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the yield of a security that pays periodic interest
      See Also:

    • yieldmat

      public static double yieldmat(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar issue, double rate, double price, DayCountBasis basis)
      Returns the annual yield of a security that pays interest at maturity. It is computed using the following:

      $${{{\left[ {1 + \left( {{{\it DIM} \over B} \times {\it rate}} \right)} \right] - \left[ {{{\it price} \over {100}} + \left( {{A \over B} \times {\it rate}} \right)} \right]} \over {{{\it price} \over {100}} + \left( {{A \over B} \times {\it rate}} \right)}}} \times {{B \over {\it DSM}}}$$

      In the equation above, \({\it DIM}\) represents the number of days in the period starting with the issue date and ending with the maturity date. \({\it DSM}\) represents the number of days in the period starting with the settlement date and ending with the maturity date. \(A\) represents the number of days in the period starting with the issue date and ending with the settlement date. \(B\) represents the number of days in a year based on the annual basis.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      issue - a GregorianCalendar issue date of the security
      rate - a double which specifies the security's interest rate at date of issue
      price - a double which specifies the security's price per $100 face value
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the annual yield of a security that pays interest at maturity
      See Also:

    • yearfrac

      public static double yearfrac(GregorianCalendar start, GregorianCalendar end, DayCountBasis basis)
      Returns the fraction of a year represented by the number of whole days between two dates. It is computed using the following:

      $$A/D$$

      where \(A\) equals the number of days from start to end, \(D\) equals annual basis.
      Parameters:
      start - a GregorianCalendar start date of the security
      end - a GregorianCalendar end date of the security
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the annual yield of a security that pays interest at maturity
      See Also:

    • yield

      public static double yield(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar issueDate, GregorianCalendar firstCoupon, double rate, double price, double redemption, int frequency, DayCountBasis basis)
      Returns the yield of a security with an odd first coupon period that pays periodic interest.

      The yield is determined by finding the zero of the function desired price - computed price, where computed price is the output of price(java.util.GregorianCalendar, java.util.GregorianCalendar, java.util.GregorianCalendar, java.util.GregorianCalendar, double, double, double, int, com.imsl.finance.DayCountBasis).

      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      issueDate - a GregorianCalendar issueDate date of the security
      firstCoupon - a GregorianCalendar first coupon date of the security
      rate - a double which specifies the security's annual coupon rate
      price - a double which specifies the security's price per $100 face value
      redemption - a double which specifies the security's redemption value per $100 face value
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the yield of a security that pays periodic interest
      See Also:

    • yield

      public static double yield(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar lastCoupon, double rate, double price, double redemption, int frequency, DayCountBasis basis)
      Returns the yield of a security with an odd last coupon period that pays periodic interest.

      The yield is determined by finding the zero of the function desired price - computed price, where computed price is the output of price(java.util.GregorianCalendar, java.util.GregorianCalendar, java.util.GregorianCalendar, double, double, double, int, com.imsl.finance.DayCountBasis).

      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      lastCoupon - a GregorianCalendar last coupon date of the security
      rate - a double which specifies the security's annual coupon rate
      price - a double which specifies the security's price per $100 face value
      redemption - a double which specifies the security's redemption value per $100 face value
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double which specifies the yield of a security that pays periodic interest
      See Also:

    • price

      public static double price(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar issueDate, GregorianCalendar firstCoupon, double rate, double yield, double redemption, int frequency, DayCountBasis basis)
      Returns the price of an odd first period coupon bond, given its yield.

      In the case of a short first period, the following formula is used:

      $$\begin{array}{lcl} P & = & \left[\frac{redemption}{\left(1+\frac{yield}{frequency}\right)^{ N-1+\frac{DSC}{E}}}\right]+\left[\frac{100*\frac{rate}{frequency}* \frac{DFC}{E}}{\left(1+\frac{yield}{frequency}\right)^\frac{DSC}{E}} \right]\\[.4cm] & + & \left[\sum^N_{K=2}\frac{100*\frac{rate}{frequency}}{\left({1+ \frac{yield}{frequency}}\right)^{K-1+\frac{DSC}{E}}}\right]-\left[100* \frac{rate}{frequency}*\frac{A}{E}\right] \end{array}$$

      where

      Variable Description
      A Number of days from the beginning of coupon period to the settlement date (accrued days).
      DFC Number of days from the beginning of odd first coupon period (issueDate) to the first coupon date.
      DSC Number of days from the settlement date to first coupon date.
      E Number of days in the quasi-coupon period in which the settlement date falls.
      N Number of coupons payable between settlement date and redemption date.

      In the case of a long first period, the following formula is used:

      $$\begin{array}{lcl} P = \left[\frac{redemption}{\left(1+\frac{yield}{frequency} \right)^{N-{Nqf}+\frac{DSC}{E}}}\right]+\left[\frac{100* \frac{rate}{frequency}*\left[\sum\limits^{NCF}_{i=1} \frac{{DFC}_i}{{NLF}_i}\right]}{\left(1+\frac{yield}{frequency} \right)^{{Nqf}+\frac{DSC}{E}}}\right]\\[.7cm] + \left[\sum^N_{K=1}\frac{100*\frac{rate}{frequency}}{\left({1+ \frac{yield}{frequency}}\right)^{K+{Nqf}+\frac{DSC}{E}}}\right]- \left[100*\frac{rate}{frequency}*\left[\sum\limits^{NCF}_{i=1} \frac{A_i}{{NLF}_i}\right]\right] \end{array}$$

      where

      Variable Description
      Ai Number of accrued days for the ith quasi-coupon period within the odd period.
      DFCi Number of days from the issueDate to the first quasi-coupon or number of days in the the quasi-coupon.
      DSC Number of days from the settlement date to the next coupon or quasi-coupon date.
      E Number of days in the quasi-coupon or coupon period in which the settlement date falls.
      N Number of coupon periods between the first real coupon date and redemption date.
      NCF Number of quasi-coupon periods that fall in the odd period.
      NLFi Number of days in the full ith quasi-coupon period within the odd period.
      Nqf Number of whole quasi-coupon periods between settlement and firstCoupon.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      issueDate - a GregorianCalendar issue date of the security
      firstCoupon - a GregorianCalendar first coupon date of the security
      rate - a double which specifies the annual coupon rate
      yield - a double which specifies the annual yield
      redemption - a double which specifies the redemption value per $100 face value
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double that indicates the bond price.
      See Also:

    • price

      public static double price(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar lastCoupon, double rate, double yield, double redemption, int frequency, DayCountBasis basis)
      Returns the price of an odd last period coupon bond, given its yield.

      In the case of a short last period with one coupon period or less to redemption, the following formula is used:

      $$P=\left[\frac{redemption+\left(\frac{100*rate}{frequency}*\frac{DLC}{E} \right)}{1+\left(\frac{DSR}{E}*\frac{yield}{frequency}\right)}\right] -\left[\frac{A}{E}*\frac{100*rate}{frequency}\right]$$

      where

      Variable Description
      A Number of days from last coupon date before redemption to settlement date.
      DLC Number of days from last coupon date before redemption to redemption.
      DSR Number of days from settlement date to redemption date.
      E Number of days in the quasi-coupon period.

      In the case of a short last period with more than one coupon period to redemption, the following formula is used:

      $$\begin{array}{lcl} P & = & \left[\frac{redemption}{\left(1+\frac{yield}{frequency} \right)^{N-1+\frac{DSC}{E}+\frac{DLC}{NLL}}}\right] & + & \left[\sum^N_{K=1}\frac{100*\frac{rate}{frequency}}{\left({1+ \frac{yield}{frequency}}\right)^{K-1+\frac{DSC}{E}}}\right]\\[.7cm] + \left[\frac{100*\frac{rate}{frequency}*\frac{DLC}{NLL}}{\left({1+ \frac{yield}{frequency}}\right)^{N-1+\frac{DSC}{E}+\frac{DLC}{NLL}}}\right]- \left[100*\frac{rate}{frequency}*\frac{A}{E}\right] \end{array}$$

      where

      Variable Description
      A Number of days from beginning of coupon period to settlement date.
      DLC Number of days from last coupon date before redemption to redemption.
      DSC Number of days from settlement date to next coupon date.
      E Number of days in coupon period in which the settlement date falls.
      N Number of coupons payable between settlement date and last coupon date before redemption.
      NLL Number of days in the full quasi-coupon period in which the odd last period falls.

      In the case of a long last period with one coupon period or less to redemption, the following formula is used:

      $$P=\left[\frac{redemption+\left(\left(\sum\limits^{NCL}_{i=1} \frac{{DLC}_i}{{NLL}_i}\right)*\frac{100*rate}{frequency} \right)}{1+\left(\sum\limits^{NCL}_{i=1}\frac{{DSC}_i}{{NLL}_i}\right)* \frac{yield}{frequency}}\right] -\left[\left(\sum\limits^{NCL}_{i=1}\frac{{A}_i}{{NLL}_i}\right)* \frac{100*rate}{frequency}\right]$$

      where

      Variable Description
      Ai Number of accrued days for the ith quasi-coupon period within the odd period counting forward from the last interest date before redemption.
      DLCi Number of days in the ith quasi-coupon period as delimited by the length of the actual coupon period.
      DSCi Number of days from settlement date (or beginning of quasi-coupon period) to next quasi-coupon within odd period (or to redemption date) for the ith quasi-coupon period.
      NCL Number of quasi-coupon periods that fit in odd period.
      NLLi Normal length in days of the full ith quasi-coupon period within odd last period.

      In the case of a long first period with more than one coupon period to redemption, the following formula is used:

      $$\begin{array}{lcl} P & = & \left[\frac{redemption}{\left(1+\frac{yield}{frequency} \right)^{N-1+\frac{DSC}{E}+Nqf+\frac{DLQ}{LQL}}}\right] & + & \left[\sum^N_{K=1}\frac{100*\frac{rate}{frequency}}{\left({1+ \frac{yield}{frequency}}\right)^{K-1+\frac{DSC}{E}}}\right]\\[.7cm] + \left[\frac{100*\frac{rate}{frequency}*\left(\sum\limits^{NCL}_{i=1} \frac{{DLC}_i}{{NLL}_i}\right)}{\left({1+\frac{yield}{frequency}} \right)^{N-1+\frac{DSC}{E}Nqf+\frac{DLQ}{LQL}}}\right]- \left[100*\frac{rate}{frequency}*\frac{A}{E}\right] \end{array}$$

      where

      Variable Description
      A Number of days from beginning of coupon period to settlement date.
      DLCi Number of days from last coupon date before redemption to first quasi-coupon or number of days in quasi-coupon.
      DLQ Number of days counted in the last quasi-coupon period within the last odd period.
      DSC Number of days from settlement date to next coupon date.
      E Number of days in coupon period in which the settlement falls.
      LQL Normal length in days of the last quasi-coupon period within the odd last period.
      N Number of coupons payable between settlement date and last coupon date before redemption.
      NCL Number of quasi-coupon periods that fit in odd period.
      NLLi Normal length in days of the full ith quasi-coupon period within odd last period.
      Nql Number of whole quasi-coupon periods between last coupon date before redemption and the redemption date.
      Parameters:
      settlement - a GregorianCalendar settlement date of the security
      maturity - a GregorianCalendar maturity date of the security
      lastCoupon - a GregorianCalendar last interest date of the security
      rate - a double which specifies the security's annual coupon rate
      yield - a double which specifies the security's annual yield
      redemption - a double which specifies the security's redemption value per $100 face value
      frequency - an int which specifies the number of coupon payments per year: ANNUAL for annual, SEMIANNUAL for semiannual, and QUARTERLY for quarterly
      basis - a DayCountBasis object which contains the type of day count basis to use. See DayCountBasis.
      Returns:
      a double that indicates the bond price.
      See Also: