Example 3

A spline interpolant

to a function

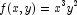is constructed. Then, the values of the partial derivative 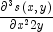$\frac{{\partial ^3 s\left( {x,y} \right)}}{{\partial x^2 2y}}$ and the error are computed on a 4 x 4 grid.

using System;
using Imsl.Math;

public class Spline2DInterpolateEx3
{
	
	private static double F(double x, double y)
	{
		return (x * x * x * y * y);
	}
	
	private static double F21(double x, double y)
	{
		return (6.0 * x * 2.0 * y);
	}
	
	public static void  Main(String[] args)
	{
		int nData = 11;
		int outData = 2;
		double[,] fData = new double[nData,nData];
		double[] xData = new double[nData];
		double[] yData = new double[nData];
		double x, y, z;
		
		// Set up grid
		for (int i = 0; i < nData; i++)
		{
			xData[i] = yData[i] = (double) i / ((double) (nData - 1));
		}
		
		for (int i = 0; i < nData; i++)
		{
			for (int j = 0; j < nData; j++)
			{
				fData[i,j] = F(xData[i], yData[j]);
			}
		}
		
		// Compute tensor-product interpolant
		Spline2DInterpolate spline = new Spline2DInterpolate(xData, yData, fData);
		
		// Print results
		Console.Out.WriteLine("   x        y     F21(x, y)   " 
		+ "21InterpDeriv   Error");
		for (int i = 0; i < outData; i++)
		{
			x = (double) (1 + i) / (double) (outData + 1);
			
			for (int j = 0; j < outData; j++)
			{
				y = (double) (1 + j) / (double) (outData + 1);
				z = spline.Derivative(x, y, 2, 1);
				Console.Out.WriteLine(x.ToString("0.0000")+"   "
					+y.ToString("0.0000")+"   "+F21(x,y).ToString("0.0000")
					+"       "+z.ToString("0.0000")+"     "
					+Math.Abs(F21(x, y) - z).ToString("0.0000"));
			}
		}
	}
}

Output

   x        y     F21(x, y)   21InterpDeriv   Error
0.3333   0.3333   1.3333       1.3333     0.0000
0.3333   0.6667   2.6667       2.6667     0.0000
0.6667   0.3333   2.6667       2.6667     0.0000
0.6667   0.6667   5.3333       5.3333     0.0000

Link to C# source.