Example 2
In this example, a two-way analysis of covariance model containing all the interaction terms is fit. First, RegressorsForGLM
is used to produce a matrix of regressors, regressors
, from the data x
. Then, regressors
is used as the input matrix into Regression
to produce the final fit. The regressors, generated using the dummy method LeaveOutLast
, are the model whose mean function is 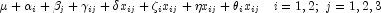 where
where 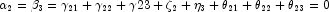 .
.
using System;
using Imsl.Stat;
using Imsl.Math;
public class RegressorsForEx2
{
public static void Main(String[] args)
{
double[,] x = {
{1.0, 1.0, 1.11},
{1.0, 1.0, 2.22},
{1.0, 1.0, 3.33},
{1.0, 2.0, 1.11},
{1.0, 2.0, 2.22},
{1.0, 2.0, 3.33},
{1.0, 3.0, 1.11},
{1.0, 3.0, 2.22},
{1.0, 3.0, 3.33},
{2.0, 1.0, 1.11},
{2.0, 1.0, 2.22},
{2.0, 1.0, 3.33},
{2.0, 2.0, 1.11},
{2.0, 2.0, 2.22},
{2.0, 2.0, 3.33},
{2.0, 3.0, 1.11},
{2.0, 3.0, 2.22},
{2.0, 3.0, 3.33}
};
double[] y = {
1.0, 2.0, 2.0, 4.0, 4.0, 6.0,
3.0, 3.5, 4.0, 4.5, 5.0, 5.5,
2.0, 3.0, 4.0, 5.0, 6.0, 7.0
};
int[][] effects = {
new int[]{0},
new int[]{1},
new int[]{0, 1},
new int[]{2},
new int[]{0, 2},
new int[]{1, 2},
new int[]{0, 1, 2}
};
int nClassVariables = 2;
RegressorsForGLM r = new RegressorsForGLM(x, nClassVariables);
r.DummyMethod = RegressorsForGLM.DummyType.LeaveOutLast;
r.SetEffects(effects);
int nRegressors = r.NumberOfRegressors;
double[,] regressors = r.GetRegressors();
Imsl.Math.PrintMatrixFormat pmf = new Imsl.Math.PrintMatrixFormat();
pmf.SetColumnLabels(new String[]{"Alpha1", "Beta1", "Beta2",
"Gamma11", "Gamma12", "Delta", "Zeta1", "Eta1", "Eta2",
"Theta11", "Theta12"});
new Imsl.Math.PrintMatrix("Regressors").Print(pmf,regressors);
LinearRegression regression = new LinearRegression(nRegressors, true);
regression.Update(regressors, y);
Console.WriteLine(" * * * Analysis of Variance * * *");
ANOVA anova = regression.ANOVA;
Object[,] table = new Object[15,2];
table[0,0] = "Degrees of freedom for the model ";
table[0,1] = anova.DegreesOfFreedomForModel;
table[1,0] = "Degrees of freedom for the error ";
table[1,1] = anova.DegreesOfFreedomForError;
table[2,0] = "Total degrees of freedom ";
table[2,1] = anova.TotalDegreesOfFreedom;
table[3,0] = "Sum of squares for the model ";
table[3,1] = anova.SumOfSquaresForModel;
table[4,0] = "Sum of squares for error ";
table[4,1] = anova.SumOfSquaresForError;
table[5,0] = "Total sum of squares ";
table[5,1] = anova.TotalSumOfSquares;
table[6,0] = "Model mean square ";
table[6,1] = anova.ModelMeanSquare;
table[7,0] = "Error mean square ";
table[7,1] = anova.ErrorMeanSquare;
table[8,0] = "F-statistic ";
table[8,1] = anova.F;
table[9,0] = "p-value ";
table[9,1] = anova.P;
table[10,0] = "R-squared ";
table[10,1] = anova.RSquared;
table[11,0] = "Adjusted R-squared ";
table[11,1] = anova.AdjustedRSquared;
table[12,0] = "Standard deviation for the model error";
table[12,1] = anova.ModelErrorStdev;
table[13,0] = "Overall mean of y ";
table[13,1] = anova.MeanOfY;
table[14,0] = "Coefficient of variation ";
table[14,1] = anova.CoefficientOfVariation;
pmf = new Imsl.Math.PrintMatrixFormat();
pmf.SetNoColumnLabels();
pmf.SetNoRowLabels();
pmf.NumberFormat = "0.0000";
new Imsl.Math.PrintMatrix().Print(pmf, table);
}
}
Output
Regressors
Alpha1 Beta1 Beta2 Gamma11 Gamma12 Delta Zeta1 Eta1 Eta2 Theta11 Theta12
0 1 1 0 1 0 1.11 1.11 1.11 0 1.11 0
1 1 1 0 1 0 2.22 2.22 2.22 0 2.22 0
2 1 1 0 1 0 3.33 3.33 3.33 0 3.33 0
3 1 0 1 0 1 1.11 1.11 0 1.11 0 1.11
4 1 0 1 0 1 2.22 2.22 0 2.22 0 2.22
5 1 0 1 0 1 3.33 3.33 0 3.33 0 3.33
6 1 0 0 0 0 1.11 1.11 0 0 0 0
7 1 0 0 0 0 2.22 2.22 0 0 0 0
8 1 0 0 0 0 3.33 3.33 0 0 0 0
9 0 1 0 0 0 1.11 0 1.11 0 0 0
10 0 1 0 0 0 2.22 0 2.22 0 0 0
11 0 1 0 0 0 3.33 0 3.33 0 0 0
12 0 0 1 0 0 1.11 0 0 1.11 0 0
13 0 0 1 0 0 2.22 0 0 2.22 0 0
14 0 0 1 0 0 3.33 0 0 3.33 0 0
15 0 0 0 0 0 1.11 0 0 0 0 0
16 0 0 0 0 0 2.22 0 0 0 0 0
17 0 0 0 0 0 3.33 0 0 0 0 0
* * * Analysis of Variance * * *
Degrees of freedom for the model 11.0000
Degrees of freedom for the error 6.0000
Total degrees of freedom 17.0000
Sum of squares for the model 43.9028
Sum of squares for error 0.8333
Total sum of squares 44.7361
Model mean square 3.9912
Error mean square 0.1389
F-statistic 28.7364
p-value 0.0003
R-squared 98.1372
Adjusted R-squared 94.7221
Standard deviation for the model error 0.3727
Overall mean of y 3.9722
Coefficient of variation 9.3821
Link to C# source.