ARMA Class

Computes least-square estimates of parameters for an ARMA model.

For a list of all members of this type, see ARMA Members.

public class ARMA

Thread Safety

Public static (Shared in Visual Basic) members of this type are safe for multithreaded operations. Instance members are not guaranteed to be thread-safe.

Remarks

Class ARMA computes estimates of parameters for a nonseasonal ARMA model given a sample of observations, $\{W_t\}$ , for $t = 1, 2, \dots, n$ , where n = z.Length. There are two methods, method of moments and least squares, from which to choose. The default is method of moments.

Two methods of parameter estimation, method of moments and least squares, are provided. The user can choose a method using the Method property. If the user wishes to use the least-squares algorithm, the preliminary estimates are the method of moments estimates by default. Otherwise, the user can input initial estimates by using the SetInitialEstimates method. The following table lists the appropriate methods and properties for both the method of moments and least-squares algorithm:

Least Squares	Both Method of Moment and Least Squares
	`Center`
`ARLags`	`Method`
`MALags`	`RelativeError`
`Backcasting`	`MaxIterations`
`ConvergenceTolerance`	`Mean`
`SetInitialEstimates`	`Mean`
`Residual`	`AutoCovariance`
`SSResidual`	`Variance`
`ParamEstimatesCovariance`	`Constant`
	`AR`
	`MA`

Method of Moments Estimation

Suppose the time series $\{Z_t\}$ is generated by an ARMA (p, q) model of the form

$\phi (B)Z_t=\theta_0+\theta(B)A_t$

${\rm {for}} \,\,\, t \in \{0, \pm 1, \pm 2, \ldots\}$

Let ${\hat \mu }= {\rm {Mean}}$ be the estimate of the mean $\mu$ of the time series $\{Z_t\}$ , where ${\hat \mu }$ equals the following:

$\hat \mu = \left\{ \begin{array}{ll} \mu & {\rm for}\;\mu\; {\rm known} \\ \frac{1}{n}\sum\limits_{t=1}^n {Z_t } & {\rm for}\;\mu\; {\rm unknown} \end{array} \right.$

The autocovariance function is estimated by

$\hat \sigma \left( k \right) = \frac{1}{n} \sum\limits_{t = 1}^{n - k} {\left( {Z_t - \hat \mu } \right)} \left( {Z_{t + k} - \hat \mu } \right)$

for $k = 0, 1, \ldots, K$ , where K = p + q. Note that ${\hat \sigma }(0)$ is an estimate of the sample variance.

Given the sample autocovariances, the function computes the method of moments estimates of the autoregressive parameters using the extended Yule-Walker equations as follows:

$\hat \Sigma \hat \phi = \hat \sigma$

where

$\hat \phi = \left( {\hat \phi _1 ,\; \ldots ,\;\hat \phi _p } \right)^T$

$\hat \Sigma _{ij} = \hat \sigma \left( {|q + i - j|} \right), \,\,\, i,j = 1, \, \ldots , \, p$

$\hat \sigma _i = \hat \sigma \left( {q + i} \right), \,\,\, i = 1,\; \ldots ,\;p$

The overall constant $\theta_0$ is estimated by the following:

$\hat \theta _0 = \left\{ \begin{array}{l} \hat \mu \,\,\, {\rm{for}} \,\, p = 0 \\ \hat \mu \left( {1 - \sum \limits_{i = 1}^p {\hat \phi _i } } \right) \,\,\, {\rm{for}} \,\, p > 0 \\ \end{array} \right.$

The moving average parameters are estimated based on a system of nonlinear equations given K = p + q + 1 autocovariances, $\sigma (k) \,\,\, {\rm{for}} \,\, k = 1, \ldots, K$ , and p autoregressive parameters $\phi_i$ for $i = 1, \ldots, p$ .

Let $Z'_t =\phi (B)Z_t$ . The autocovariances of the derived moving average process $Z'_t =\theta(B)A_t$ are estimated by the following relation:

$\hat \sigma '\left( k \right) = \left\{ \begin{array}{l} \hat \sigma \left( k \right) \,\,\, {\rm{for}} \,\, p = 0 \\ \sum\limits_{i = 0}^p {\sum\limits_{j = 0}^p {\hat \phi _i \hat \phi _j } \left( {\hat \sigma \left( {\left| {k + i - j} \right|} \right)} \right) \,\,\,\, {\rm{for}} \,\,\, p \ge 1,\hat \phi _0 \equiv - 1} \\ \end{array} \right.$

The iterative procedure for determining the moving average parameters is based on the relation

$\sigma \left( k \right) = \left\{ \begin{array}{l} \left( {1 + \theta _1^2 + \; \ldots \; + \theta _q^2 } \right)\sigma _A^2 \,\,\,\, {\rm{for}} \,\,\, k = 0 \\ \left( { - \theta _k + \theta _1 \theta _{k + 1} + \; \ldots \; + \theta _{q - k} \theta _q } \right)\sigma _A^2 \,\,\,\, {\rm{for}} \,\,\, k \ge 1 \\ \end{array} \right.$

where $\sigma (k)$ denotes the autocovariance function of the original process.

Let $\tau = (\tau_0, \tau_1, \ldots , \tau_q)^T$ and $f = (f_0, f_1, \dots, f_q)^T$ , where

$\tau _j = \left\{ \begin{array}{l} \sigma _A \,\,\,\, {\rm{for}} \,\,\, j = 0 \\ - \theta _j /\tau _0 \,\,\,\, {\rm{for}} \,\,\, j = 1,\; \ldots ,\;q \\ \end{array} \right.$

and

$f_j = \sum\limits_{i = 0}^{q - j} {\tau _i } \tau _{i + j} - \hat \sigma '\left( j \right) \,\,\,\, {\rm{for}} \,\,\, j = 0,\;1,\; \ldots ,\;q$

Then, the value of $\tau$ at the (i + 1)-th iteration is determined by the following:

$\tau ^{i + 1} = \tau ^i - \left( {T^i } \right)^{ - 1} f^i$

The estimation procedure begins with the initial value

$\tau ^0 = (\sqrt {\hat \sigma '\left( 0 \right),} \quad 0,\; \ldots ,\;0)^T$

and terminates at iteration i when either $\left\| {f^i } \right\|$ is less than RelativeError or i equals MaxIterations. The moving average parameter estimates are obtained from the final estimate of $\tau$ by setting

$\hat \theta _j = - \tau _j /\tau _0 \,\,\,\, {\rm{for}} \,\,\, j = 1,\; \ldots ,\;q$

The random shock variance is estimated by the following:

$\hat \sigma _A^2 = \left\{ \begin{array}{l} \hat \sigma (0) - \sum\limits_{i = 1}^p {\hat \phi _i \hat \sigma (i) \,\,\,\, {\rm{for}} \,\,\, q = 0} \\ \tau _0^2 \,\,\,\, {\rm{for}} \,\,\, q \ge 0 \\ \end{array} \right.$

See Box and Jenkins (1976, pp. 498-500) for a description of a function that performs similar computations.

Least-squares Estimation

Suppose the time series $\{Z_t\}$ is generated by a nonseasonal ARMA model of the form,

$\phi (B) (Z_t - \mu) = \theta(B)A_t \,\,\,\, {\rm{for}} \,\,t \in \{0, \pm 1, \pm 2, \ldots\}$

where B is the backward shift operator, $\mu$ is the mean of , and

$\phi \left( B \right) = 1 - \phi _1 B^{l_\phi \left( 1 \right)} - \phi _2 B^{l_\phi \left( 2 \right)} - \;...\; - \phi _p B^{l_\phi \left( p \right)} \quad \,\,\,\, {\rm{for}} \,\,\, p \ge 0$

${\rm{\theta }}\left( B \right) = 1 - {\rm{\theta }}_1 B^{l_\theta \left( 1 \right)} - {\rm{\theta }}_2 B^{l_\theta \left( 2 \right)} - \;...\; - {\rm{\theta }}_q B^{l_\theta \left( q \right)} \quad \,\,\,\, {\rm{for}} \,\,\, q \ge 0$

with p autoregressive and q moving average parameters. Without loss of generality, the following is assumed:

$1 \leq l_\phi (1) \leq l_\phi (2) \leq \ldots \leq l_\phi (p)$

$1 \leq l_\theta (1) \leq l_\theta (2) \leq \ldots \leq l_\theta (q)$

so that the nonseasonal ARMA model is of order , where $p' = l_\theta (p)$ and $q' = l_\theta (q)$ . Note that the usual hierarchical model assumes the following:

$l_\phi (i) = i, 1 \le i \le p$

$l_\theta (j) = j, 1 \le j \le q$

Consider the sum-of-squares function

$S_T \left( {\mu ,\phi ,\theta } \right) = \sum\limits_{ - T + 1}^n {\left[ {A_t } \right]^2 }$

where

$\left[ {A_t } \right] = E\left[ {A_t \left| {\left( {\mu ,\phi ,\theta ,Z} \right)} \right.} \right]$

and T is the backward origin. The random shocks $\{A_t\}$ are assumed to be independent and identically distributed

$N \left( {0,\sigma _A^2 } \right)$

random variables. Hence, the log-likelihood function is given by

$l\left( {\mu ,\phi ,\theta ,\sigma _A } \right) = f\left( {\mu ,\phi ,\theta } \right) - n\ln \left( {\sigma _A } \right) - \frac{{S_T \left( {\mu ,\phi ,\theta } \right)}} {{2\sigma _A^2 }}$

where $f (\mu, \phi, \theta)$ is a function of $\mu, \phi, {\rm{and}} \, \theta$ .

For T = 0, the log-likelihood function is conditional on the past values of both and required to initialize the model. The method of selecting these initial values usually introduces transient bias into the model (Box and Jenkins 1976, pp. 210-211). For $T = \infty$ , this dependency vanishes, and estimation problem concerns maximization of the unconditional log-likelihood function. Box and Jenkins (1976, p. 213) argue that

$S_\infty \left( {\mu ,\phi ,\theta } \right)/\left( {2\sigma _A^2 } \right)$

dominates

$l\left( {\mu ,\phi ,\theta ,\sigma _A^2 } \right)$

The parameter estimates that minimize the sum-of-squares function are called least-squares estimates. For large n, the unconditional least-squares estimates are approximately equal to the maximum likelihood-estimates.

In practice, a finite value of T will enable sufficient approximation of the unconditional sum-of-squares function. The values of needed to compute the unconditional sum of squares are computed iteratively with initial values of obtained by back forecasting. The residuals (including backcasts), estimate of random shock variance, and covariance matrix of the final parameter estimates also are computed. ARIMA parameters can be computed by using Difference with ARMA.

Forecasting

The Box-Jenkins forecasts and their associated probability limits for a nonseasonal ARMA model are computed given a sample of n = z.Length, $\{Z_t\}$ for $t = 1, 2, \ldots, n$ .

Suppose the time series is generated by a nonseasonal ARMA model of the form

$\phi (B)Z_t = \theta_0 + \theta(B)A_t$

for $t \in \left\{ {0, \pm 1,\, \pm 2,\, \ldots } \right\}$ , where B is the backward shift operator, $\theta_0$ is the constant, and

$\phi \left( B \right) = 1 - \phi _1 B^{l_\phi \left( 1 \right)} - \phi _2 B^{l_\phi \left( 2 \right)} - \; \ldots \; - \phi _p B^{l_\phi \left( p \right)}$

$\theta \left( B \right) = 1 - \theta _1 B^{l_\theta \left( 1 \right)} - \theta _2 B^{l_\theta \left( 2 \right)} - \; \ldots \; - \theta _q B^{l_\theta \left( q \right)}$

with p autoregressive and q moving average parameters. Without loss of generality, the following is assumed:

$1 \leq l_\phi(1) \leq l_\phi (2) \leq \ldots l_\phi (p)$

$1 \leq l_\theta (1) \leq l_\theta (2) \leq \ldots \leq l_\theta (q)$

so that the nonseasonal ARMA model is of order , where ${p'}= l_\theta(p)$ and ${q'}= l_\theta(q)$ . Note that the usual hierarchical model assumes the following:

$l_\phi (i) = i, 1 \leq i \leq p$

$l_\theta (j) = j, 1 \leq j \leq q$

The Box-Jenkins forecast at origin t for lead time l of $Z_{t+1}$ is defined in terms of the difference equation

$\hat Z_t \left( l \right) = \theta _0 + \phi _1 \left[ {Z_{t + l - l_\phi \left( 1 \right)} } \right] + \; \ldots \; + \phi _p \left[ {Z_{t + l - l_\phi \left( p \right)} } \right]$

$+ \left[ {A_{t + l} } \right] - \theta _1 \left[ {A_{t + l - l_\theta \left( 1 \right)} } \right]\; - \;...\; - \;\left[ {A_{t + l} } \right] - \theta _1 \left[ {A_{t + l - l \theta \left( 1 \right)} } \right] - ... - \theta _q \left[ {A_{t + l - l_\theta \left( q \right)} } \right]$

where the following is true:

$\left[ {Z_{t + k} } \right] = \left\{ \begin{array}{l}Z_{t + k} \,\,\,\, {\rm{for}} \,\,\, k = 0,\; - 1,\; - 2,\; \ldots \\ \hat Z_t \left( k \right) \,\,\,\, {\rm{for}} \,\,\, k = 1,\;2,\; \ldots \\ \end{array} \right.$

$\left[ {A_{t + k} } \right] = \left\{ \begin{array}{l} Z_{t + k} - \hat Z_{t + k - 1} \left( 1 \right) \,\,\,\, {\rm{for}} \,\,\, k = 0,\; - 1,\; - 2,\;... \\ 0 \,\,\,\, {\rm{for}} \,\,\, k = 1,\;2,\;... \\ \end{array} \right.$

The $100(1 - \alpha)$ percent probability limits for $Z_{t+l}$ are given by

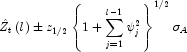
$\hat Z_t \left( l \right) \pm z_{1/2} \left\{ {1 + \sum\limits_{j = 1}^{l - 1} {\psi _j^2 } } \right\}^{1/2} \sigma _A$

where $z_{(1-\alpha/2)}$ is the $100(1 - \alpha/2)$ percentile of the standard normal distribution

$\sigma _A^2$

and

$\left\{ {\psi _j^2 } \right\}$

are the parameters of the random shock form of the difference equation. Note that the forecasts are computed for lead times $l = 1, 2, \ldots, L$ at origins $t = (n - b), (n - b + 1), \ldots, n$ , where $L = {\rm nForecast}$ and $b = {\rm BackwardOrigin}$ .

The Box-Jenkins forecasts minimize the mean-square error

$E\left[ {Z_{t + l} - \hat Z_t \left( l \right)} \right]^2$

Also, the forecasts can be easily updated according to the following equation:

$\hat Z_{t + 1} \left( l \right) = \hat Z_t \left( {l + 1} \right) + \psi _l A_{t + 1}$

This approach and others are discussed in Chapter 5 of Box and Jenkins (1976).

Requirements

Namespace: Imsl.Stat

Assembly: ImslCS (in ImslCS.dll)

ARMA Class

Thread Safety

Remarks

Requirements

See Also