Cdf.ComplementaryChi Method

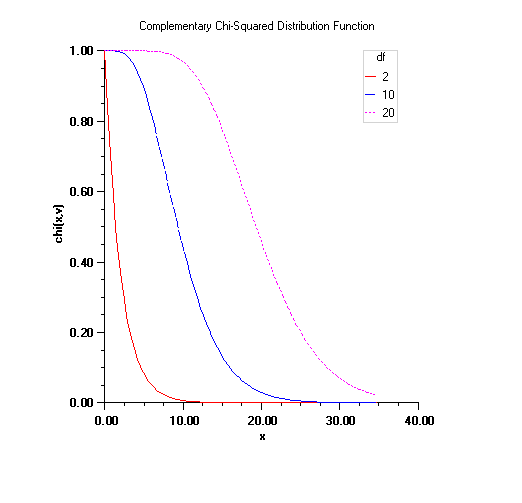
Calculates the complement of the chi-squared distribution.

public static double ComplementaryChi(
double chsq,
double df
);

Parameters

chsq: A double scalar value at which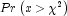 $Pr \left( x \gt \chi ^2 \right)$ is to be evaluated.
df: A double specifying the number of degrees of freedom. This must be at least 0.5.

Return Value

A double specifying the probability that a chi-squared random variable takes a value greater than chsq.

Remarks

Method ComplementaryChi evaluates the distribution function, , of a chi-squared random variable with df degrees of freedom, that is, with $v = {\rm df}$ , and $x = {\rm chsq}$ ,

$F\left( x \right) = \frac{1}{{2^{\nu /2} \Gamma \left( {\nu /2} \right)}} \int_0^x {e^{ - t/2} t^{\nu /2 - 1} } dt$

where $\Gamma (\cdot)$ is the gamma function. The value of the distribution function at the point x is the probability that the random variable takes a value greater than x.

For $v \gt 343$ , ComplementaryChi uses the Wilson-Hilferty approximation (Abramowitz and Stegun 1964, equation 26.4.17) to the one minus the normal distribution, and method Normal is used to evaluate the normal distribution function.

For $v \le 343$ , ComplementaryChi uses series expansions to evaluate the distribution function. If $x \lt \max (v/2, 26)$ , ComplementaryChi uses the series 6.5.29 in Abramowitz and Stegun (1964), otherwise, it uses the asymptotic expansion 6.5.32 in Abramowitz and Stegun.

This function provides higher right tail accuracy for the Chi-squared distribution.

Plot of the Complementary Chi-Squared Distribution Function

Cdf.ComplementaryChi Method

Parameters

Return Value

Remarks

See Also