Cdf.ExtremeValue Method

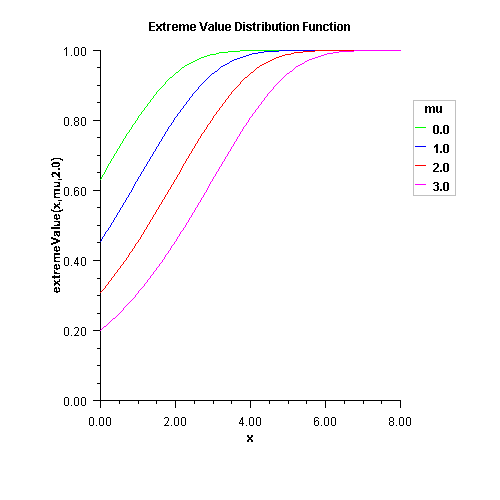
Evaluates the extreme value cumulative probability distribution function.

public static double ExtremeValue(
   double x,
   double mu,
   double beta
);

Parameters

x: A double scalar value representing the argument at which the function is to be evaluated.
mu: A double scalar value representing the location parameter, $\mu$ .
beta: A double scalar value representing the scale parameter, $\beta$ .

Return Value

A double scalar value representing the probability that an extreme value random variable takes on a value less than or equal to x.

Remarks

Method ExtremeValue, also known as the Gumbel minimum distribution, evaluates the extreme value distribution function, F, of a uniform random variable with location parameter $\mu$ and shape parameter $\beta$ ; that is,

$F\left( x \right) = \int_0^x {1 - e^{ - e^{\frac{x-\mu}{\beta}}}} dt$

The case where $\mu =0$ and $\beta = 1$ is called the standard Gumbel distribution.

Random numbers are generated by evaluating uniform variates , equating the continuous distribution function, and then solving for by first computing $\frac{x_i - \mu}{\beta}=log(-log(1-u_i))$ .

Plot of Extreme Value Distribution Function

Cdf.ExtremeValue Method

Parameters

Return Value

Remarks

See Also