Cdf.Noncentralchi Method

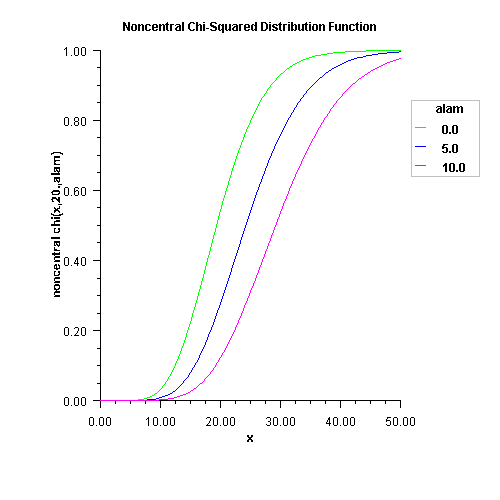
Evaluates the noncentral chi-squared cumulative probability distribution function.

public static double Noncentralchi(
   double chsq,
   double df,
   double alam
);

Parameters

chsq: A double scalar value representing the argument at which the function is to be evaluated.
df: A double scalar value representing the number of degrees of freedom. This must be at least 0.5.
alam: A double scalar value representing the noncentrality parameter. This must be nonnegative, and alam + df must be less than or equal to 200,000.

Return Value

A double scalar value representing the probability that a chi-squared random variable takes a value less than or equal to chsq.

Remarks

Method Noncentralchi evaluates the distribution function, F, of a noncentral chi-squared random variable with df degrees of freedom and noncentrality parameter alam, that is, with $\nu = {\rm df}$ , $\lambda = {\rm alam}$ , and $x = {\rm chsq}$ ,

$F\left( x \right) = \sum\limits_{i = 0}^\infty {\frac{e^{-\lambda/2}\left(\lambda/2\right)^i}{i!}} \int_0^x {\frac{t^{\left(\nu + 2i\right)/2-1}e^{ - t/2}} {2^{\left(\nu+2i\right)/2}{\Gamma\left(\frac{\nu+2i}{2}\right)}}} dt$

where $\Gamma (\cdot)$ is the gamma function. This is a series of central chi-squared distribution functions with Poisson weights. The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.

The noncentral chi-squared random variable can be defined by the distribution function above, or alternatively and equivalently, as the sum of squares of independent normal random variables. If the have independent normal distributions with means ${\mu}_i$ and variances equal to one and

$X = \sum\limits_{i = 1}^n{Y_i}^2$

then has a noncentral chi-squared distribution with degrees of freedom and noncentrality parameter equal to

$\sum\limits_{i = 1}^n{\mu_i}^2$

With a noncentrality parameter of zero, the noncentral chi-squared distribution is the same as the chi-squared distribution.

Noncentralchi determines the point at which the Poisson weight is greatest, and then sums forward and backward from that point, terminating when the additional terms are sufficiently small or when a maximum of 1000 terms have been accumulated. The recurrence relation 26.4.8 of Abramowitz and Stegun (1964) is used to speed the evaluation of the central chi-squared distribution functions.

Noncentral Chi-Squared Distribution Function

Cdf.Noncentralchi Method

Parameters

Return Value

Remarks

See Also