NonlinearRegression Class

Fits a multivariate nonlinear regression model using least squares.

For a list of all members of this type, see NonlinearRegression Members.

System.Object
Imsl.Stat.NonlinearRegression

public class NonlinearRegression

Thread Safety

Public static (Shared in Visual Basic) members of this type are safe for multithreaded operations. Instance members are not guaranteed to be thread-safe.

Remarks

The nonlinear regression model is

$y_i=f(x_i;\theta)+\varepsilon_i\,\,\,\,\,\,\, \,\,\,i=1,\,2,\,\ldots,\,n$

where the observed values of the constitute the responses or values of the dependent variable, the known are vectors of values of the independent (explanatory) variables, $\theta$ is the vector of regression parameters, and the $\varepsilon_i$ are independently distributed normal errors each with mean zero and variance $\sigma^2$ . For this model, a least squares estimate of $\theta$ is also a maximum likelihood estimate of $\theta$ .

The residuals for the model are

$e_i(\theta)=y_i-f(x_i;\theta)\,\,\,\,\,\,\,\, \,\,i=1,\,2,\,\ldots,\,n$

A value of $\theta$ that minimizes

$\sum\limits_{i=1}^n[e_i(\theta)]^2$

is the least-squares estimate of $\theta$ calculated by this class. NonlinearRegression accepts these residuals one at a time as input from a user-supplied function. This allows NonlinearRegression to handle cases where

is so large that data cannot reside in an array but must reside in a secondary storage device.

NonlinearRegression is based on MINPACK routines LMDIF and LMDER by More' et al. (1980). NonlinearRegression uses a modified Levenberg-Marquardt method to generate a sequence of approximations to the solution. Let $\hat\theta_c$ be the current estimate of $\theta$ . A new estimate is given by

$\hat \theta_c + s_c$

where

is a solution to

$(J(\hat\theta_c)^T J(\hat\theta_c)+\mu_c I) s_c = J(\hat \theta_c)^T e(\hat \theta_c)$

Here, $J(\hat\theta_c)$ is the Jacobian evaluated at $\hat\theta_c$ .

The algorithm uses a "trust region" approach with a step bound of $\hat\delta_c$ . A solution of the equations is first obtained for $\mu_c=0$ . If $||s_c||_2\lt \delta_c$ , this update is accepted; otherwise, $\mu_c$ is set to a positive value and another solution is obtained. The method is discussed by Levenberg (1944), Marquardt (1963), and Dennis and Schnabel (1983, pages 129 - 147, 218 - 338).

Forward finite differences are used to estimate the Jacobian numerically unless the user supplied function computes the derivatives. In this case the Jacobian is computed analytically via the user-supplied function.

NonlinearRegression does not actually store the Jacobian but uses fast Givens transformations to construct an orthogonal reduction of the Jacobian to upper triangular form. The reduction is based on fast Givens transformations (see Golub and Van Loan 1983, pages 156-162, Gentleman 1974). This method has two main advantages:

The loss of accuracy resulting from forming the crossproduct matrix used in the equations for is avoided.
The n x p Jacobian need not be stored saving space when .

A weighted least squares fit can also be performed. This is appropriate when the variance of $\epsilon_i$ in the nonlinear regression model is not constant but instead is $\sigma^2/w_i$ . Here, are weights input via the user supplied function. For the weighted case, NonlinearRegression finds the estimate by minimizing a weighted sum of squares error.

Programming Notes

Nonlinear regression allows users to specify the model's functional form. This added flexibility can cause unexpected convergence problems for users who are unaware of the limitations of the algorithm. Also, in many cases, there are possible remedies that may not be immediately obvious. The following is a list of possible convergence problems and some remedies. No one-to-one correspondence exists between the problems and the remedies. Remedies for some problems may also be relevant for the other problems.

A local minimum is found. Try a different starting value. Good starting values can often be obtained by fitting simpler models. For example, for a nonlinear function
$f(x;\theta) = \theta_1e^{\theta_2x}$
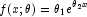
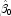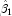good starting values can be obtained from the estimated linear regression coefficients $\hat\beta_0$ and $\hat\beta_1$ from a simple linear regression of ln y on ln x. The starting values for the nonlinear regression in this case would be
$\theta_1=e^{\hat\beta_0}\,and\,\theta_2= \hat\beta_1$
If an approximate linear model is unclear, then simplify the model by reducing the number of nonlinear regression parameters. For example, some nonlinear parameters for which good starting values are known could be set to these values. This simplifies the approach to computing starting values for the remaining parameters.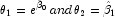
The estimate of is incorrectly returned as the same or very close to the initial estimate.
- The scale of the problem may be orders of magnitude smaller than the assumed default of 1 causing premature stopping. For example, if the sums of squares for error is less than approximately 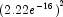${(2.22e^{-16})}^2$ , the routine stops. See Example 3, which shows how to shut down some of the stopping criteria that may not be relevant for your particular problem and which also shows how to improve the speed of convergence by the input of the scale of the model parameters.
- The scale of the problem may be orders of magnitude larger than the assumed default causing premature stopping. The information with regard to the input of the scale of the model parameters in Example 3 is also relevant here. In addition, the maximum allowable step size MaxStepsize in Example 3 may need to be increased.
- The residuals are input with accuracy much less than machine accuracy, causing premature stopping because a local minimum is found. Again see Example 3 to see how to change some default tolerances. If you cannot improve the precision of the computations of the residual, you need to use method Digits to indicate the actual number of good digits in the residuals.
The model is discontinuous as a function of $\theta$ . There may be a mistake in the user-supplied function. Note that the function 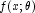$f(x;\theta)$ can be a discontinuous function of x.
The R matrix value given by R is inaccurate. If only a function is supplied try providing the NonlinearRegression.IDerivative. If the derivative is supplied try providing only NonlinearRegression.IFunction.
Overflow occurs during the computations. Make sure the user-supplied functions do not overflow at some value of $\theta$ .
The estimate of $\theta$ is going to infinity. A parameterization of the problem in terms of reciprocals may help.
Some components of $\theta$ are outside known bounds. This can sometimes be handled by making a function that produces artificially large residuals outside of the bounds (even though this introduces a discontinuity in the model function).

Note that the Solve method must be called before using any property as a right operand, otherwise the value is null.

Requirements

Namespace: Imsl.Stat

Assembly: ImslCS (in ImslCS.dll)

NonlinearRegression Class

Thread Safety

Remarks

Programming Notes

Requirements

See Also