Random.NextHypergeometric Method

Generate a pseudorandom number from a hypergeometric distribution.

public virtual int NextHypergeometric(
   int n,
   int m,
   int l
);

Parameters

n: A int which specifies the number of items in the sample,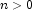 $n \gt 0$ .
m: A int which specifies the number of special items in the population, or lot,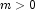 $m \gt 0$ .
l: A int which specifies the number of items in the lot,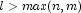 $l \gt max(n,m)$ .

Return Value

A int which specifies the number of special items in a sample of size n drawn without replacement from a population of size l that contains m such special items.

Remarks

Method NextHypergeometric generates pseudorandom numbers from a hypergeometric distribution with parameters n, m, and l. The hypergeometric random variable x can be thought of as the number of items of a given type in a random sample of size n that is drawn without replacement from a population of size l containing m items of this type. The probability function is

$f\left( x \right) = \frac{{\left( {_x^m } \right)\left( {_{n - x}^{l - m} } \right)}}{{\left( {_n^l } \right)}}$

for $x = {\rm max}(0, n - l + m), 1, 2, \ldots, {\rm min}(n, m)$ .

If the hypergeometric probability function with parameters n, m, and l evaluated at n - l + m (or at 0 if this is negative) is greater than the machine epsilon, and less than 1.0 minus the machine epsilon, then NextHypergeometric uses the inverse CDF technique. The method recursively computes the hypergeometric probabilities, starting at $x = {\rm max}(0, n - l + m)$ and using the ratio f (x = x + 1)/f(x = x) (see Fishman 1978, page 457).

If the hypergeometric probability function is too small or too close to 1.0, then NextHypergeometric generates integer deviates uniformly in the interval , for $i = 0, 1, \ldots$ ; and at the I-th step, if the generated deviate is less than or equal to the number of special items remaining in the lot, the occurrence of one special item is tallied and the number of remaining special items is decreased by one. This process continues until the sample size or the number of special items in the lot is reached, whichever comes first. This method can be much slower than the inverse CDF technique. The timing depends on n. If n is more than half of l (which in practical examples is rarely the case), the user may wish to modify the problem, replacing n by l - n, and to consider the deviates to be the number of special items not included in the sample.

Random.NextHypergeometric Method

Parameters

Return Value

Remarks

See Also