Example 5: Hessian Approximation
This example uses the same data as in the One-Sided Differences example. In this example numerical differentiation is used to approximate the Hessian matrix of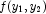 
. This symmetric Hessian matrix is ![Hf = \left[ {\begin{array}{*{20}c} {\frac{{\partial ^2 f}} {{\partial y_1^2 }}} & {\frac{{\partial ^2 f}} {{\partial y_1 \partial y_2 }}} \\ {\frac{{\partial ^2 f}} {{\partial y_1 \partial y_2 }}} & {\frac{{\partial ^2 f}} {{\partial y_2^2 }}} \\ \end{array} } \right]](eqn/eqn_0342.png)
Our method is based on casting the matrix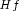 
as the 2 by 2 Jacobian matrix of the gradient function. Each inner evaluation of the gradient function is itself computed using NumericalDerivatives
. Central differences are used for both the inner and outer numerical differentiation. Because of the inherent error in both processes, the expected accuracy is about the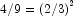 
power of machine precision. Note that the approximation obtained is not symmetric. However, the difference between the off-diagonal elements provides an error estimate of that term.
using System;
using Imsl.Math;
public class NumericalDerivativesEx5 : NumericalDerivatives
{
static int m = 1, n = 2;
static double a, b, c, v = 0.0;
class NumericalDerivativesFcn : NumericalDerivatives.IFunction
{
private int num;
public NumericalDerivativesFcn(int num)
{
this.num = num;
}
public double[] F(int varIndex, double[] y)
{
return new double[num];
}
}
class InnerNumericalDerivatives : NumericalDerivatives
{
public InnerNumericalDerivatives(NumericalDerivatives.IFunction fcn) :
base(fcn)
{
}
// Override EvaluateF.
public override double[] EvaluateF(int varIndex, double[] y)
{
double[] valueF = new double[m];
valueF[0] = a * Math.Exp(b * y[0]) + c * y[0] * y[1] * y[1];
return valueF;
}
}
public NumericalDerivativesEx5(NumericalDerivatives.IFunction fcn) :
base(fcn)
{
}
// Override EvaluateF.
public override double[] EvaluateF(int varIndex, double[] y)
{
NumericalDerivatives.DifferencingMethod[] iopt =
new NumericalDerivatives.DifferencingMethod[n];
double[] valueF = new double[m];
double[] scale = new double[n];
double[] fac = new double[n];
// This is the analytic gradient. for comparison only.
// stateh(1)=a*b*exp(b*y(1))+c*y(2)**2
// stateh(2)=2*c*y(1)*y(2)
//
// Each request for a gradient evaluation uses the
// functionality of numerical evaluation, but with
// the same numerical code.
iopt[0] = NumericalDerivatives.DifferencingMethod.Central;
iopt[1] = NumericalDerivatives.DifferencingMethod.Central;
// Set the increment used at the default value.
// Set defaults for increments and scaling:
fac[0] = 1.4901161193847656E-8;
fac[1] = 1.4901161193847656E-8;
// Change scale to account for large value of a.
switch (varIndex)
{
case 1:
scale[0] = 1.0e0;
scale[1] = 8.0e8;
break;
case 2:
scale[0] = 1.0e4;
scale[1] = 8.0e8;
break;
}
InnerNumericalDerivatives derv =
new InnerNumericalDerivatives(new NumericalDerivativesFcn(m));
derv.SetPercentageFactor(fac);
derv.SetDifferencingMethods(iopt);
derv.SetScalingFactors(scale);
derv.SetInitialF(valueF);
double[,] fjac = derv.EvaluateJ(y);
// Since the function is never evaluated at the
// initial point, hold back until the request is made.
// Copy gradient value into array expected by
// outer loop computing the Hessian matrix.
double[] tmp = new double[n];
for (int i = 0; i < n; i++)
{
tmp[i] = fjac[0, i];
}
return tmp;
}
public static void Main(String[] args)
{
NumericalDerivatives.DifferencingMethod[] iopth =
new NumericalDerivatives.DifferencingMethod[n];
double u;
double[] fach = new double[n];
double[] stateh = new double[n];
double[] scaleh = new double[n];
double[,] actual = new double[n, n];
double[] y = new double[n];
// Define data and point of evaluation:
a = 2.5e6;
b = 3.4e0;
c = 4.5e0;
y[0] = 2.1e0;
y[1] = 3.2e0;
// Machine precision, for measuring errors
u = 2.220446049250313e-016;
// Compute expected relative error using two applications
// of central differences.
v = Math.Pow(3.0e0 * u, 2.0e0 / 3.0e0);
v = Math.Pow(3 * v, 2.0 / 3.0);
// Set increments and scaling:
fach[0] = 1.4901161193847656E-8;
fach[1] = 1.4901161193847656E-8;
iopth[0] = NumericalDerivatives.DifferencingMethod.Central;
iopth[1] = NumericalDerivatives.DifferencingMethod.Central;
// Compute true values of partials.
actual[0, 0] = a * b * b * Math.Exp(b * y[0]);
actual[1, 0] = 2 * c * y[1];
actual[0, 1] = 2 * c * y[1];
actual[1, 1] = 2 * c * y[0];
// Set the increment used at the default value.
scaleh[0] = 1;
scaleh[1] = 8.0e5;
NumericalDerivativesEx5 derv2 =
new NumericalDerivativesEx5(new NumericalDerivativesFcn(n));
derv2.SetPercentageFactor(fach);
derv2.SetDifferencingMethods(iopth);
derv2.SetScalingFactors(scaleh);
derv2.SetInitialF(stateh);
double[,] h = derv2.EvaluateJ(y);
PrintMatrixFormat pmf = new PrintMatrixFormat();
pmf.NumberFormat = "0.00";
new PrintMatrix("Numerical Hessian:").Print(pmf, h);
new PrintMatrix("Analytic Hessian:").Print(pmf, actual);
// Since the function is never evaluated at the
// initial point, hold back until the request is made.
// Subtract the actual hessian matrix values and check.
h[0, 0] = (h[0, 0] - actual[0, 0]) / h[0, 0] / v;
h[1, 0] = (h[1, 0] - actual[1, 0]) / h[1, 0] / v;
h[0, 1] = (h[0, 1] - actual[0, 1]) / h[0, 1] / v;
h[1, 1] = (h[1, 1] - actual[1, 1]) / h[1, 1] / v;
pmf.NumberFormat = "0.000";
new PrintMatrix("Hessian Matrix, Expected Normalized " +
"Relative Error, |all entries|").Print(pmf, h);
}
}
Output
Numerical Hessian:
0 1
0 36455292905.82 28.80
1 28.80 18.90
Analytic Hessian:
0 1
0 36455280444.94 28.80
1 28.80 18.90
Hessian Matrix, Expected Normalized Relative Error, |all entries|
0 1
0 0.914 0.037
1 0.036 0.000
Link to C# source.