Example 1: CrossCorrelation
Consider the Gas Furnace Data (Box and Jenkins 1976, pages 532-533) where X
is the input gas reate in cubic feet/minute and Y
is the percent 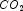 in the outlet gas. The
in the outlet gas. The CrossCorrelation
methods GetCrossCovariance
and GetCrossCorrelation
are used to compute the cross-covariances and cross-correlations between time series X
and Y
with lags from -maximumLag
= -10 through lag maximumLag
= 10. In addition, the estimated standard errors of the estimated cross-correlations are computed. In the first invocation of method GetStandardErrors
stderrMethod = Bartletts
, the standard errors are based on the assumption that autocorrelations and cross-correlations for lags greater than maximumLag
or less than -maximumLag
are zero. In the second invocation of method GetStandardErrors
with stderrMethod
= BartlettsNoCC
, the standard errors are based on the additional assumption that all cross-correlations for X
and Y
are zero.
using System;
using Imsl.Stat;
using PrintMatrix = Imsl.Math.PrintMatrix;
public class CrossCorrelationEx1
{
public static void Main(String[] args)
{
double[] x2 = new double[]{100.8, 81.6, 66.5, 34.8, 30.6,
7, 19.8, 92.5, 154.4, 125.9,
84.8, 68.1, 38.5, 22.8, 10.2,
24.1, 82.9, 132, 130.9, 118.1,
89.9, 66.6, 60, 46.9, 41,
21.3, 16, 6.4, 4.1, 6.8,
14.5, 34, 45, 43.1, 47.5,
42.2, 28.1, 10.1, 8.1, 2.5,
0, 1.4, 5, 12.2, 13.9,
35.4, 45.8, 41.1, 30.4, 23.9,
15.7, 6.6, 4, 1.8, 8.5,
16.6, 36.3, 49.7, 62.5, 67,
71, 47.8, 27.5, 8.5, 13.2,
56.9, 121.5,138.3, 103.2, 85.8,
63.2, 36.8, 24.2, 10.7, 15,
40.1, 61.5, 98.5, 124.3, 95.9,
66.5, 64.5, 54.2, 39, 20.6,
6.7, 4.3, 22.8, 54.8, 93.8,
95.7, 77.2, 59.1, 44, 47,
30.5, 16.3, 7.3, 37.3, 73.9};
double[] x = new double[]{- 0.109, 0.0, 0.178, 0.339, 0.373,
0.441, 0.461, 0.348, 0.127,
- 0.18, - 0.588, - 1.055, - 1.421,
- 1.52, - 1.302, - 0.814, - 0.475,
- 0.193, 0.088, 0.435, 0.771,
0.866, 0.875, 0.891, 0.987, 1.263,
1.775, 1.976, 1.934, 1.866, 1.832,
1.767, 1.608, 1.265, 0.79, 0.36,
0.115, 0.088, 0.331, 0.645, 0.96,
1.409, 2.67, 2.834, 2.812, 2.483,
1.929, 1.485, 1.214, 1.239, 1.608,
1.905, 2.023, 1.815, 0.535, 0.122,
0.009, 0.164, 0.671, 1.019, 1.146,
1.155, 1.112, 1.121, 1.223, 1.257,
1.157, 0.913, 0.62, 0.255, - 0.28,
- 1.08, - 1.551, - 1.799, - 1.825,
- 1.456, - 0.944, - 0.57, - 0.431,
- 0.577, - 0.96, - 1.616, - 1.875,
- 1.891, - 1.746, - 1.474, - 1.201,
- 0.927, - 0.524, 0.04, 0.788,
0.943, 0.93, 1.006, 1.137, 1.198,
1.054, 0.595, - 0.08, - 0.314,
- 0.288, - 0.153, - 0.109, - 0.187,
- 0.255, - 0.229, - 0.007, 0.254,
0.33, 0.102, - 0.423, - 1.139,
- 2.275, - 2.594, - 2.716, - 2.51,
- 1.79, - 1.346, - 1.081, - 0.91,
- 0.876, - 0.885, - 0.8, - 0.544,
- 0.416, - 0.271, 0.0, 0.403,
0.841, 1.285, 1.607, 1.746, 1.683,
1.485, 0.993, 0.648, 0.577, 0.577,
0.632, 0.747, 0.9, 0.993, 0.968,
0.79, 0.399, - 0.161, - 0.553,
- 0.603, - 0.424, - 0.194, - 0.049,
0.06, 0.161, 0.301, 0.517, 0.566,
0.56, 0.573, 0.592, 0.671, 0.933,
1.337, 1.46, 1.353, 0.772, 0.218,
- 0.237, - 0.714, - 1.099, -1.269,
- 1.175, - 0.676, 0.033, 0.556,
0.643, 0.484, 0.109, - 0.31, -0.697,
- 1.047, - 1.218, - 1.183, -0.873,
-0.336, 0.063, 0.084, 0.0, 0.001,
0.209, 0.556, 0.782, 0.858, 0.918,
0.862, 0.416, - 0.336, - 0.959,
- 1.813, - 2.378, - 2.499, -2.473,
- 2.33, - 2.053, - 1.739, - 1.261,
- 0.569, - 0.137, - 0.024, - 0.05,
- 0.135, - 0.276, - 0.534, -0.871,
- 1.243, - 1.439, - 1.422, -1.175,
- 0.813, - 0.634, - 0.582, -0.625,
- 0.713, - 0.848, - 1.039, -1.346,
- 1.628, - 1.619, - 1.149, -0.488,
- 0.16, - 0.007, - 0.092, - 0.62,
- 1.086, - 1.525, - 1.858, -2.029,
- 2.024, - 1.961, - 1.952, -1.794,
- 1.302, - 1.03, - 0.918, - 0.798,
- 0.867, - 1.047,- 1.123, - 0.876,
- 0.395, 0.185, 0.662, 0.709,
0.605, 0.501, 0.603, 0.943, 1.223,
1.249, 0.824, 0.102, 0.025, 0.382,
0.922, 1.032, 0.866, 0.527, 0.093,
- 0.458, - 0.748, - 0.947, -1.029,
- 0.928, - 0.645, - 0.424, -0.276,
- 0.158, - 0.033, 0.102, 0.251,
0.28, 0.0, -0.493, -0.759, -0.824,
- 0.74, - 0.528, - 0.204, 0.034,
0.204, 0.253, 0.195, 0.131, 0.017,
- 0.182, - 0.262};
double[] y = new double[]{53.8, 53.6, 53.5, 53.5, 53.4, 53.1,
52.7, 52.4, 52.2, 52.0, 52.0,
52.4, 53.0, 54.0, 54.9, 56.0,
56.8, 56.8, 56.4, 55.7, 55.0,
54.3, 53.2, 52.3, 51.6, 51.2,
50.8, 50.5, 50.0, 49.2, 48.4,
47.9, 47.6, 47.5, 47.5, 47.6,
48.1, 49.0, 50.0, 51.1, 51.8,
51.9, 51.7, 51.2, 50.0, 48.3,
47.0, 45.8, 45.6, 46.0, 46.9,
47.8, 48.2, 48.3, 47.9, 47.2,
47.2, 48.1, 49.4, 50.6, 51.5,
51.6, 51.2, 50.5, 50.1, 49.8,
49.6, 49.4, 49.3, 49.2, 49.3,
49.7, 50.3, 51.3, 52.8, 54.4,
56.0, 56.9, 57.5, 57.3, 56.6,
56.0, 55.4, 55.4, 56.4, 57.2,
58.0, 58.4, 58.4, 58.1, 57.7,
57.0, 56.0, 54.7, 53.2, 52.1,
51.6, 51.0, 50.5, 50.4, 51.0,
51.8, 52.4, 53.0, 53.4, 53.6,
53.7, 53.8, 53.8, 53.8, 53.3,
53.0, 52.9, 53.4, 54.6, 56.4,
58.0, 59.4, 60.2, 60.0, 59.4,
58.4, 57.6, 56.9, 56.4, 56.0,
55.7, 55.3, 55.0, 54.4, 53.7,
52.8, 51.6, 50.6, 49.4, 48.8,
48.5, 48.7, 49.2, 49.8, 50.4,
50.7, 50.9, 50.7, 50.5, 50.4,
50.2, 50.4, 51.2, 52.3, 53.2,
53.9, 54.1, 54.0, 53.6, 53.2,
53.0, 52.8, 52.3, 51.9, 51.6,
51.6, 51.4, 51.2, 50.7, 50.0,
49.4, 49.3, 49.7, 50.6, 51.8,
53.0, 54.0, 55.3, 55.9, 55.9,
54.6, 53.5, 52.4, 52.1, 52.3,
53.0, 53.8, 54.6, 55.4, 55.9,
55.9, 55.2, 54.4, 53.7, 53.6,
53.6, 53.2, 52.5, 52.0, 51.4,
51.0, 50.9, 52.4, 53.5, 55.6,
58.0, 59.5, 60.0, 60.4, 60.5,
60.2, 59.7, 59.0, 57.6, 56.4,
55.2, 54.5, 54.1, 54.1, 54.4,
55.5, 56.2, 57.0, 57.3, 57.4,
57.0, 56.4, 55.9, 55.5, 55.3,
55.2, 55.4, 56.0, 56.5, 57.1,
57.3, 56.8, 55.6, 55.0, 54.1,
54.3, 55.3, 56.4, 57.2, 57.8,
58.3, 58.6, 58.8, 58.8, 58.6,
58.0, 57.4, 57.0, 56.4, 56.3,
56.4, 56.4, 56.0, 55.2, 54.0,
53.0, 52.0, 51.6, 51.6, 51.1,
50.4, 50.0, 50.0, 52.0, 54.0,
55.1, 54.5, 52.8, 51.4, 50.8,
51.2, 52.0, 52.8, 53.8, 54.5,
54.9, 54.9, 54.8, 54.4, 53.7,
53.3, 52.8, 52.6, 52.6, 53.0,
54.3, 56.0, 57.0, 58.0, 58.6,
58.5, 58.3, 57.8, 57.3, 57.0};
CrossCorrelation cc = new CrossCorrelation(x, y, 10);
Console.Out.WriteLine("Mean = " + cc.MeanX);
Console.Out.WriteLine("Mean = " + cc.MeanY);
Console.Out.WriteLine("Xvariance = " + cc.VarianceX);
Console.Out.WriteLine("Yvariance = " + cc.VarianceY);
new PrintMatrix
("CrossCovariances are: ").Print(cc.GetCrossCovariances());
new PrintMatrix
("CrossCorrelations are: ").Print(cc.GetCrossCorrelations());
double[] stdErrors =
cc.GetStandardErrors(CrossCorrelation.StdErr.Bartletts);
new PrintMatrix
("Standard Errors using Bartlett are: ").Print(stdErrors);
stdErrors =
cc.GetStandardErrors(CrossCorrelation.StdErr.BartlettsNoCC);
new PrintMatrix("Standard Errors using Bartlett #2 are: ").Print
(stdErrors);
new PrintMatrix("AutoCovariances of X are: ").Print
(cc.GetAutoCovarianceX());
new PrintMatrix("AutoCovariances of Y are: ").Print
(cc.GetAutoCovarianceY());
new PrintMatrix("AutoCorrelations of X are: ").Print
(cc.GetAutoCorrelationX());
new PrintMatrix("AutoCorrelations of Y are: ").Print
(cc.GetAutoCorrelationY());
}
}
Output
Mean = -0.0568344594594595
Mean = 53.5091216216216
Xvariance = 1.14693790165038
Yvariance = 10.2189370662893
CrossCovariances are:
0
0 -0.404501563294314
1 -0.508490782763824
2 -0.614369467627782
3 -0.705476130258359
4 -0.776166564117932
5 -0.831473609098764
6 -0.891315326970392
7 -0.980605209560792
8 -1.12477059434257
9 -1.34704305203341
10 -1.65852650999817
11 -2.04865124574232
12 -2.48216585776478
13 -2.88541054192018
14 -3.16536049680239
15 -3.25343758942199
16 -3.13112860301494
17 -2.83919398544463
18 -2.45302186901565
19 -2.05268794195849
20 -1.6946546517713
CrossCorrelations are:
0
0 -0.118153717307789
1 -0.148528662561878
2 -0.179455515102209
3 -0.206067503381416
4 -0.226715971265165
5 -0.242870996488244
6 -0.260350586329711
7 -0.286431898500946
8 -0.3285421835153
9 -0.39346731487308
10 -0.484450717109386
11 -0.598405005361053
12 -0.725033348897091
13 -0.842819935503927
14 -0.924592494205792
15 -0.950319553992448
16 -0.914593458680361
17 -0.829320215245049
18 -0.716520475473708
19 -0.599584112456951
20 -0.495003641096017
Standard Errors using Bartlett are:
0
0 0.158147783754555
1 0.155750271182418
2 0.152735096430409
3 0.149086745416716
4 0.145054998300008
5 0.141300099196058
6 0.138420534019813
7 0.136074039397204
8 0.132158917844376
9 0.123531347020305
10 0.107879045104545
11 0.0873410658167485
12 0.0641407975847026
13 0.0469456102701398
14 0.0440970262220149
15 0.0482335854893665
16 0.0491545707033738
17 0.0475621871011123
18 0.0534780426550682
19 0.0715660938138719
20 0.0939330263600716
Standard Errors using Bartlett #2 are:
0
0 0.162753654681801
1 0.162469864309526
2 0.162187553298139
3 0.161906708839297
4 0.161627318279375
5 0.161349369117073
6 0.16107284900106
7 0.160797745727675
8 0.160524047238664
9 0.160251741618955
10 0.159980817094486
11 0.160251741618955
12 0.160524047238664
13 0.160797745727675
14 0.16107284900106
15 0.161349369117073
16 0.161627318279375
17 0.161906708839297
18 0.162187553298139
19 0.162469864309526
20 0.162753654681801
AutoCovariances of X are:
0
0 1.14693790165038
1 1.09242958215267
2 0.956651878489968
3 0.782050821478561
4 0.609290776371371
5 0.467379623909361
6 0.36495658921123
7 0.298426970727032
8 0.260942845999682
9 0.244377603086156
10 0.238942463361545
AutoCovariances of Y are:
0
0 10.2189370662893
1 9.92010118439122
2 9.15657243817617
3 8.09900196442277
4 6.94850770962479
5 5.87055032023953
6 4.96076244327211
7 4.25188969596136
8 3.73611877936647
9 3.37615547781905
10 3.13231605775447
AutoCorrelations of X are:
0
0 1
1 0.952474916541448
2 0.834092130980584
3 0.681859776674248
4 0.531232576318765
5 0.407502117801518
6 0.31820082733867
7 0.26019453215175
8 0.227512619143721
9 0.213069602752258
10 0.208330776250152
AutoCorrelations of Y are:
0
0 1
1 0.970756656983059
2 0.896039615351222
3 0.79254837483442
4 0.67996384208558
5 0.574477588242088
6 0.485447988483746
7 0.416079448222429
8 0.365607377277169
9 0.330382255602345
10 0.306520730819207
Link to C# source.