Computes the solution of a sparse real symmetric positive definite system of linear equations 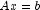Ax=b.

Namespace: Imsl.Math
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.0.0

Syntax

C#
public double[] Solve(
	double[] b
)
Visual Basic (Declaration)
Public Function Solve ( _
	b As Double() _
) As Double()
Visual C++
public:
array<double>^ Solve(
	array<double>^ b
)

Parameters

b
Type: array< System..::.Double >[]()[]
A double vector of length equal to the order of matrix A representing the right-hand side of the linear system.

Return Value

A double vector of length equal to the order of matrix A representing the solution to the system of linear equations Ax=b.

Remarks

This method solves the linear system Ax=b, where A is symmetric positive definite. The solution is obtained in several steps:

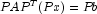  1. First, matrix A is permuted to reduce fill-in, leading to a sparse symmetric positive definite system PAP^T(Px)=Pb.
  2. Then, matrix 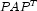PAP^T is symbolically and numerically factored.
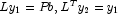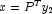  3. The final solution is obtained by solving the systems Ly_1=Pb, L^Ty_2=y_1 and x=P^Ty_2.

By default this method implements all of the above steps. The factorizations are retained for later use by subsequent solves. By choosing appropriate methods within this class, the computation can be reduced to the solution of the system Ax=b for a given or precomputed symbolic or numeric factor.

Exceptions

ExceptionCondition
Imsl.Math..::.NotSPDException is thrown when the input matrix is not symmetric, positive definite.

See Also