Evaluates the noncentral beta cumulative probability distribution function
(CDF).
Namespace:
Imsl.Stat
Assembly:
ImslCS (in ImslCS.dll) Version: 6.5.0.0
 Syntax
Syntax
| C# |
|---|
public static double NoncentralBeta( double x, double shape1, double shape2, double lambda ) |
| Visual Basic (Declaration) |
|---|
Public Shared Function NoncentralBeta ( _ x As Double, _ shape1 As Double, _ shape2 As Double, _ lambda As Double _ ) As Double |
| Visual C++ |
|---|
public: static double NoncentralBeta( double x, double shape1, double shape2, double lambda ) |
Parameters
- x
- Type: System..::.Double
A double scalar value representing the argument at which the function is to be evaluated. x must be nonnegative and less than or equal to 1.
- shape1
- Type: System..::.Double
A double scalar value representing the first shape parameter. shape1 must be positive.
- shape2
- Type: System..::.Double
A double scalar value representing the second shape parameter. shape2 must be positive.
- lambda
- Type: System..::.Double
A double scalar value representing the noncentrality parameter. lambda must nonnegative.
Return Value
A double scalar value representing the probability that a noncentral beta random variable takes a value less than or equal to x. Remarks
Remarks
The noncentral beta distribution is a generalization of the beta
distribution. If  is a noncentral chi-square
random variable with noncentrality parameter
is a noncentral chi-square
random variable with noncentrality parameter  and
and 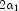 degrees of freedom,
and
degrees of freedom,
and  is a chi-square random variable with
is a chi-square random variable with
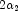 degrees of freedom which is
statistically independent of
degrees of freedom which is
statistically independent of  , then
, then
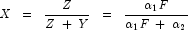 is a noncentral beta-distributed random variable and
is a noncentral beta-distributed random variable and
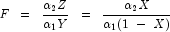 is a noncentral F-distributed random variable. The CDF for
noncentral beta variable X can thus be simply defined in
terms of the noncentral F CDF:
is a noncentral F-distributed random variable. The CDF for
noncentral beta variable X can thus be simply defined in
terms of the noncentral F CDF:
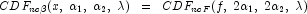 where
where 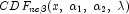 is the noncentral beta CDF with
is the noncentral beta CDF with  = x,
= x, 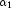 =
shape1,
=
shape1, 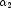 =
shape2, and noncentrality parameter
=
shape2, and noncentrality parameter  = lambda;
= lambda; 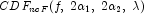 is the noncentral
F CDF with argument f, numerator and denominator degrees of
freedom
is the noncentral
F CDF with argument f, numerator and denominator degrees of
freedom 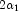 and
and 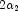 respectively, and noncentrality parameter
respectively, and noncentrality parameter  ; and:
; and:
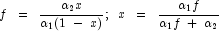 (See documentation for class Cdf method NoncentralF
for a discussion of how the noncentral F CDF is defined and
calculated.)
(See documentation for class Cdf method NoncentralF
for a discussion of how the noncentral F CDF is defined and
calculated.)
With a noncentrality parameter of zero, the noncentral beta distribution is the same as the beta distribution.