Namespace:
Imsl.Math
Assembly:
ImslCS (in ImslCS.dll) Version: 6.5.0.0
 Syntax
Syntax
| C# |
|---|
[SerializableAttribute] public class ComplexSparseCholesky |
| Visual Basic (Declaration) |
|---|
<SerializableAttribute> _ Public Class ComplexSparseCholesky |
| Visual C++ |
|---|
[SerializableAttribute] public ref class ComplexSparseCholesky |
 Remarks
Remarks
Class ComplexSparseCholesky computes the Cholesky factorization
of a sparse Hermitian positive definite matrix A. This
factorization can then be used to compute the solution of the linear
system ![]() .
.
Typically, the solution of a large sparse positive definite system
![]() is done in four steps.
is done in four steps.
- In step one, an ordering algorithm is used to preserve sparsity in the Cholesky factor L of matrix A during the numerical factorization process. The new order can be described by a permutation matrix P.
- Step two consists of
setting up the data structure for the Cholesky factor L, where
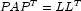 . This step is called the symbolic
factorization phase of the computation. During symbolic factorization, only
the sparsity pattern of sparse matrix A, i.e., the locations of the
nonzero entries of matrix A are needed but not any of the elements
themselves.
. This step is called the symbolic
factorization phase of the computation. During symbolic factorization, only
the sparsity pattern of sparse matrix A, i.e., the locations of the
nonzero entries of matrix A are needed but not any of the elements
themselves. - In step 3, the numerical factorization phase, the Cholesky factorization is done numerically.
- Step 4 is the solution phase.
Here, the numerical solution, x, to the original system is obtained
by solving the two triangular systems
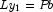 ,
,
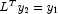 and the permutation
and the permutation
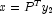 .
.
Class ComplexSparseCholesky realizes all four steps by algorithms described in George and Liu (1981). Especially, step one, is a realization of a minimum degree ordering algorithm. The numerical factorization in its standard form is based on a sparse compressed storage scheme. Alternatively, a multifrontal method can be used. The multifrontal method requires more storage but will be faster than the standard method in certain cases. The multifrontal method is based on the routines in Liu (1987). For a detailed description of this method, see Liu (1990), also Duff and Reid(1983, 1984), Ashcraft (1987) et al. (1987), and Liu (1986, 1989, 1992). The numerical factorization method can be specified by using the NumericFactorizationMethod property.
The Solve method will compute the symbolic and numeric factorizations if they have not already been computed or supplied by the user through the FactorSymbolically, FactorNumerically, SetNumericFactor, or SetSymbolicFactor methods. These factorizations are retained for later use by the Solve method when different right-hand sides are to be solved.
There is a special situation where computations can be simplified.If an application generates different sparse Hermitian positive definite coefficient matrices that all have the same sparsity pattern, then by using methods GetSymbolicFactor and SetSymbolicFactor the symbolic factorization needs only be computed once.