Syntax

C#
[SerializableAttribute] public class MinConNLP

Visual Basic (Declaration)
<SerializableAttribute> _ Public Class MinConNLP

Visual C++
[SerializableAttribute] public ref class MinConNLP

Remarks

MinConNLP is based on the FORTRAN subroutine, DONLP2, by Peter Spellucci and licensed from TU Darmstadt. MinConNLP uses a sequential equality constrained quadratic programming method with an active set technique, and an alternative usage of a fully regularized mixed constrained subproblem in case of nonregular constraints (i.e. linear dependent gradients in the "working sets"). It uses a slightly modified version of the Pantoja-Mayne update for the Hessian of the Lagrangian, variable dual scaling and an improved Armjijo-type stepsize algorithm. Bounds on the variables are treated in a gradient-projection like fashion. Details may be found in the following two papers:

P. Spellucci: An SQP method for general nonlinear programs using only equality constrained subproblems. Math. Prog. 82, (1998), 413-448.

P. Spellucci: A new technique for inconsistent problems in the SQP method. Math. Meth. of Oper. Res. 47, (1998), 355-500. (published by Physica Verlag, Heidelberg, Germany).

The problem is stated as follows:

$\mathop {\min }\limits_{x\; \in \;R^n } f\left ( x \right)$

subject to

${\rm{ }}g_j \left( x \right) = 0, {\rm{for}} \,\, j = 1,\; \ldots ,\;m_e$

$g_j \left( x \right) \ge 0, \rm{for} \,\, {j = m_e + 1,\; \ldots ,\;m}$

$x_l \le x \le x_u$

where all problem functions are assumed to be continuously differentiable. Although default values are provided for optional input arguments, it may be necessary to adjust these values for some problems. Through the use of member functions, MinConNLP allows for several parameters of the algorithm to be adjusted to account for specific characteristics of problems. The DONLP2 Users Guide provides detailed descriptions of these parameters as well as strategies for maximizing the performance of the algorithm. In addition, the following are a number of guidelines to consider when using MinConNLP:

A good initial starting point is very problem specific and should be provided by the calling program whenever possible. See method SetGuess.
Gradient approximation methods can have an effect on the success of MinConNLP. Selecting a higher order approximation method may be necessary for some problems. See property DifferentiationType.
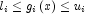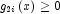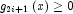If a two sided constraint $l_i \le g_i \left( x \right) \le u_i$ is transformed into two constraints, $g_{2i} \left( x \right) \ge 0$ and $g_{2i+1} \left( x \right) \ge 0$ , then choose 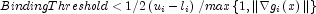$BindingThreshold \lt 1/2 \left( u_i-l_i \right)/max \left\{ 1,\|\nabla g_i \left( x \right) \| \right\}$ , or at least try to provide an estimate for that value. This will increase the efficiency of the algorithm. See property BindingThreshold.
The parameter ierr provided in the interface to the user supplied function F can be very useful in cases when evaluation is requested at a point that is not possible or reasonable. For example, if evaluation at the requested point would result in a floating point exception, then setting ierr to true and returning without performing the evaluation will avoid the exception. MinConNLP will then reduce the stepsize and try the step again. Note, if ierr is set to true for the initial guess, then an error is issued.

Inheritance Hierarchy

System..::.Object
Imsl.Math..::.MinConNLP

Syntax

Remarks

Inheritance Hierarchy

See Also