Namespace:
Imsl.Stat
Assembly:
ImslCS (in ImslCS.dll) Version: 6.5.0.0
 Syntax
Syntax
| C# |
|---|
[SerializableAttribute] public class ARMAOutlierIdentification |
| Visual Basic (Declaration) |
|---|
<SerializableAttribute> _ Public Class ARMAOutlierIdentification |
| Visual C++ |
|---|
[SerializableAttribute] public ref class ARMAOutlierIdentification |
 Remarks
Remarks
Consider a univariate time series ![]() that can be described by the
following multiplicative seasonal ARIMA model of order
that can be described by the
following multiplicative seasonal ARIMA model of order ![]() :
:
Outlier detection and parameter estimation
In general, ![]() is not directly observable due to the influence of outliers.
Chen and Liu (1993) distinguish between four types of outliers: innovational outliers (IO), additive
outliers (AO), temporary changes (TC) and level shifts (LS). If an outlier occurs as the last observation
of the series, then Chen and Liu's algorithm is unable to determine the outlier's classification. In
class ARMAOutlierIdentification, such an outlier is called a UI (unable to identify) and
is treated as an innovational outlier.
is not directly observable due to the influence of outliers.
Chen and Liu (1993) distinguish between four types of outliers: innovational outliers (IO), additive
outliers (AO), temporary changes (TC) and level shifts (LS). If an outlier occurs as the last observation
of the series, then Chen and Liu's algorithm is unable to determine the outlier's classification. In
class ARMAOutlierIdentification, such an outlier is called a UI (unable to identify) and
is treated as an innovational outlier.
In order to take the effects of multiple outliers occurring at time points ![]() into account, Chen and Liu consider the following model:
into account, Chen and Liu consider the following model:
The last formula shows that the outlier free series ![]() can be obtained from the
original series
can be obtained from the
original series ![]() by removing all occurring outlier effects:
by removing all occurring outlier effects:
-
 for an innovational outlier,
for an innovational outlier, -
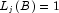 for an additive outlier,
for an additive outlier, -
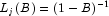 for a level shift outlier and
for a level shift outlier and -
 for a temporary change outlier.
for a temporary change outlier.
Class ARMAOutlierIdentification is an implementation of Chen and Liu's algorithm. It determines
the coefficients in ![]() and
and ![]() and the outlier effects
in the model for the observed series jointly in three stages. The magnitude of the outlier effects is determined
by least squares estimates. Outlier detection itself is realized by examination of the maximum value of the
standardized statistics of the outlier effects. For a detailed description, see Chen and Liu's original
paper (1993).
and the outlier effects
in the model for the observed series jointly in three stages. The magnitude of the outlier effects is determined
by least squares estimates. Outlier detection itself is realized by examination of the maximum value of the
standardized statistics of the outlier effects. For a detailed description, see Chen and Liu's original
paper (1993).
Intermediate and final estimates for the coefficients in ![]() and
and ![]() are computed by the Compute methods from classes ARMA and ARMAMaxLikelihood.
If the roots of
are computed by the Compute methods from classes ARMA and ARMAMaxLikelihood.
If the roots of ![]() or
or ![]() lie on or within the unit circle, then
the algorithm stops with an appropriate exception. In this case, different values for p and q should be tried.
lie on or within the unit circle, then
the algorithm stops with an appropriate exception. In this case, different values for p and q should be tried.
Forecasting
From the relation between original and outlier free series,
- Computation of the forecasts for the outlier free series
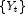 .
. - Computation of the forecasts for the original series
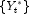 by adding the multiple outlier effects to the forecasts for
by adding the multiple outlier effects to the forecasts for 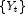 .
.
Step 1: Computation of the forecasts for the outlier free series ![]()
Since
Step 2: Computation of the forecasts for the original series ![]() by adding the multiple outlier effects to the forecasts for
by adding the multiple outlier effects to the forecasts for ![]()
The formulas for ![]() for the different types of outliers are as follows:
for the different types of outliers are as follows:
Innovational outlier (IO)
Additive outliers (AO)
Level shifts (LS)
Temporary changes (TC)
Innovational outliers (IO)
Additive outliers (AO)
Level shifts (LS)
Temporary changes (TC)