Computes the sample cross-correlation function of two stationary time series.

Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.0.0

Syntax

C#
[SerializableAttribute]
public class CrossCorrelation
Visual Basic (Declaration)
<SerializableAttribute> _
Public Class CrossCorrelation
Visual C++
[SerializableAttribute]
public ref class CrossCorrelation

Remarks

CrossCorrelation estimates the cross-correlation function of two jointly stationary time series given a sample of n = x.Length observations \{X_t\} and \{Y_t\} for t = 1,2, ..., n.

Let

\hat \mu _x = \rm{xmean}
be the estimate of the mean \mu _X of the time series \{X_t\} where
\hat \mu _X = \left\{ \begin{array}{ll} \mu _X & {\rm for}\;\mu _X\; {\rm known} \\ \frac{1}{n}\sum\limits_{t=1}^n {X_t } & {\rm for}\; \mu _X\; {\rm unknown} \end{array} \right.

The autocovariance function of \{X_t\}, \sigma _X(k), is estimated by

\hat \sigma _X\left( k \right) = \frac{1}{n} \sum\limits_{t = 1}^{n - k} {\left( {X_t - \hat \mu _X} \right)} \left( {X_{t + k} - \hat \mu _X} \right), \mbox{\hspace{20pt}k=0,1,\dots,K}
where K = maximumLag. Note that \hat \sigma _X(0) is equivalent to the sample variance of x returned by property VarianceX. The autocorrelation function \rho _X(k) is estimated by
\hat\rho _X(k) = \frac{\hat \sigma _X(k)}{\hat \sigma _X(0)},\mbox{\hspace{20pt}} k=0,1,\dots,K

Note that \hat \rho _x(0) \equiv 1 by definition. Let

\hat \mu _Y = {\rm ymean}, \hat \sigma _Y(k), {\rm and} \hat \rho _Y(k)
be similarly defined.

The cross-covariance function \sigma _{XY}(k) is estimated by

\hat \sigma _{XY}(k) = \left\{ \begin{array}{ll} \frac{1}{n}\sum\limits_{t=1}^{n-k}(X_t - {\hat \mu _X})(Y_{t+k} - {\hat\mu _Y}) & {k = 0,1, \dots,K} \\ \frac{1}{n}\sum\limits_{t=1-k}^{n}(X_t - {\hat \mu _X})(Y_{t+k} - {\hat\mu _Y}) &{k = -1,-2, \dots,-K} \end {array} \right.
The cross-correlation function \rho _{XY}(k) is estimated by
\hat \rho _{XY}(k) = \frac{\hat \sigma _{XY}(k)} {[\hat\sigma _X(0) \hat\sigma _Y(0) ]^{\frac{1}{2}}} \;\;\; {k = 0,\pm1, \dots,\pm K}

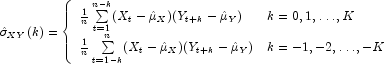
The standard errors of the sample cross-correlations may be optionally computed according to the GetStandardErrors method argument stderrMethod. One method is based on a general asymptotic expression for the variance of the sample cross-correlation coefficient of two jointly stationary time series with independent, identically distributed normal errors given by Bartlet (1978, page 352). The theoretical formula is

\begin{array}{c} {\rm var} \left \{ \hat \rho _{XY}(k) \right \} = \frac{1}{n-k}\sum\limits_{i=-\infty}^{\infty} \left [\right. {\rho _X(i)}+\rho _{XY}(i-k)\rho _{XY}(i+k) \\ -2\rho _{XY}(k)\{\rho _X(i)\rho _{XY}(i+k)+\rho _{XY}(-i)\rho _Y(i+k)\} \\ +\rho^2_{XY}(k)\{\rho_X(i) + \frac{1}{2}\rho^2_X(i) + \frac{1}{2}\rho^2_Y(i)\} \left. \right ] \end{array}
For computational purposes, the autocorrelations \rho_X(k) and \rho_Y(k) and the cross-correlations \rho _{XY}(k) are replaced by their corresponding estimates for \left|k\right|\le K, and the limits of summation are equal to zero for all k such that \left|k\right| > K.

A second method evaluates Bartlett's formula under the additional assumption that the two series have no cross-correlation. The theoretical formula is

{\rm var}\{\hat \rho_{XY}(k)\} = \frac{1}{n-k}\sum\limits_{i=-\infty}^{\infty}{\rho_X(i)\rho_Y(i)} \;\;\;\;\; {k \ge 0}
For additional special cases of Bartlett's formula, see Box and Jenkins (1976, page 377).

An important property of the cross-covariance coefficient is \sigma _{XY}(k) = \sigma _{YX}(-k) for k \ge 0. This result is used in the computation of the standard error of the sample cross-correlation for lag k \lt 0. In general, the cross-covariance function is not symmetric about zero so both positive and negative lags are of interest.

Inheritance Hierarchy

System..::.Object
Imsl.Stat..::.CrossCorrelation

See Also