Gridded Contour Chart

Example: Contour Chart from Gridded Data

In the restricted three-body problem, two large objects (masses

and

) a distance a apart, undergoing mutual gravitational attraction, circle a common center-of-mass. A third small object (mass m ) is assumed to move in the same plane as

and

and is assumed to be two small to affect the large bodies. For simplicity, we use a coordinate system that has the center of mass at the origin.

and

are on the x -axis at

and

, respectively.

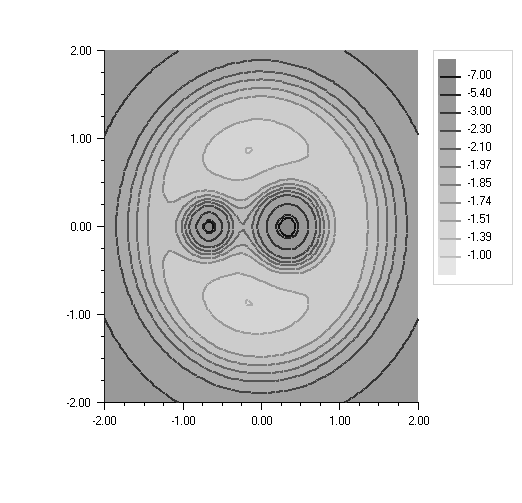
In the center-of-mass coordinate system, the effective potential energy of the system is given by

$V= \frac{m(M_1+M_2)G}{a} \left[ \frac{x_2}{\sqrt{(x-x_1)^2+y^2}} - \frac{x_1}{\sqrt{(x-x_2)^2+y^2}} - \frac{1}{2}\left( x^2+y^2 \right) \right]$ The universal gravitational constant is G . The following program plots the part of V(x,y) inside of the square bracket. The factor $\frac{m(M_1+M_2)G}{a}$ is ignored because it just scales the plot.

using Imsl.Chart2D;
using System;
using System.Windows.Forms;

public class ContourEx1 : FrameChart 
{
    public ContourEx1() 
    {
        Chart chart = this.Chart;

        int nx = 80;
        int ny = 80;
        
        // Allocate space
        double[] xGrid = new double[nx];
        double[] yGrid = new double[ny];
        double[,] zData = new double[nx,ny];
        
        // Setup the grids points
        for (int i = 0; i < nx; i++)
        {
            xGrid[i] = - 2 + 4.0 * i / (double) (nx - 1);
        }
        for (int j = 0; j < ny; j++)
        {
            yGrid[j] = - 2 + 4.0 * j / (double) (ny - 1);
        }
        
        // Evaluate the function at the grid points
        for (int i = 0; i < nx; i++)
        {
            for (int j = 0; j < ny; j++)
            {
                double x = xGrid[i];
                double y = yGrid[j];
                double rm = 0.5;
                double x1 = rm / (1.0 + rm);
                double x2 = x1 - 1.0;
                double d1 = System.Math.Sqrt((x - x1) * (x - x1) + y * y);
                double d2 = System.Math.Sqrt((x - x2) * (x - x2) + y * y);
                zData[i,j] = x2 / d1 - x1 / d2 - 0.5 * (x * x + y * y);
            }
        }
        
        // Create the contour chart, with user-specified levels and a legend
        AxisXY axis = new AxisXY(chart);
        double[] cLevel = new double[]{-7, -5.4, -3, -2.3, -2.1, -1.97, -1.85,
                                       -1.74, -1.51, -1.39, -1};
        Contour c = new Contour(axis, xGrid, yGrid, zData, cLevel);
        c.ContourLegend.IsVisible = true;

    }

    public static void Main(string[] argv) 
    {
        System.Windows.Forms.Application.Run(new ContourEx1());
    }
}

Output

Link to C# source.