Example 3: Three-way Analysis of Variance

This example performs a three-way analysis of variance using data discussed by John (1971, pp. 91 92). The responses are weights (in grams) of roots of carrots grown with varying amounts of applied nitrogen ( A), potassium ( B), and phosphorus ( C). Each cell of the three-way layout has one response. Note that the ABC interactions sum of squares, which is 186, is given incorrectly by John (1971, Table 5.2.) The three-way layout is given in the following table:

�
�
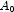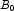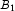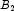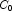	88.76	91.41	97.85
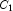	87.45	98.27	95.85
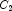	86.01	104.20	90.09

�
�
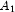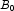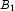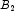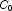	94.83	100.49	99.75
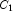	84.57	97.20	112.30
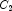	81.06	120.80	108.77

�
�
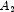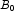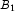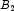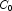	99.90	100.23	104.50
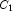	92.98	107.77	110.94
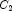	94.72	118.39	102.87

using System;
using Imsl.Stat;

public class ANOVAFactorialEx3
{
    public static void  Main(String[] args)
    {
        int nSubscripts = 3, i;
        int[] nLevels = new int[]{3, 3, 3};
        double[] y = new double[]{   88.76, 87.45, 86.01,
                                     91.41, 98.27, 104.2, 
                                     97.85, 95.85, 90.09, 
                                     94.83, 84.57, 81.06, 
                                     100.49, 97.2, 120.8, 
                                     99.75, 112.3, 108.77,
                                     99.9, 92.98, 94.72,
                                     100.23, 107.77, 118.39, 
                                     104.51, 110.94, 102.87};
        String[] labels = 
            new String[]{"degrees of freedom for the model" + 
            "                 ", "degrees of freedom for error" +
            "                      ", 
            "total (corrected) degrees of freedom             ", 
            "sum of squares for the model                  ", 
            "sum of squares for error                        ", 
            "total (corrected) sum of squares              ", 
            "model mean square                               ", 
            "error mean square                                ",
            "F-statistic                                       ", 
           "p-value                                           ", 
           "R-squared (in percent)                           ", 
           "Adjusted R-squared (in percent)                  ", 
           "est. standard deviation of the model error        ", 
           "overall mean of y                                ", 
           "coefficient of variation (in percent)             "};
        String[] rlabels = 
            new String[]{"A", "B", "C", "A*B", "A*C", "B*C"};

        ANOVAFactorial af = 
            new ANOVAFactorial(nSubscripts, nLevels, y);
        
        af.ErrorIncludeType = ANOVAFactorial.ErrorCalculation.Pooled;
        Console.Out.WriteLine
            ("P-value = " + af.Compute().ToString("0.000000"));
        
        Console.Out.WriteLine
            ("\n          * * * Analysis of Variance * * *");
        double[] anova = af.GetANOVATable();
        for (i = 0; i < anova.Length; i++)
        {
            Console.Out.WriteLine
                (labels[i] + " " + anova[i].ToString("0.0000"));
        }
        
        Console.Out.WriteLine
            ("\n          * * * Variation Due to the " + "Model * * *");
        Console.Out.WriteLine
            ("Source\tDF\tSum of Squares\tMean Square" + 
             "\tProb. of Larger F");
        double[,] te = af.GetTestEffects();
        for (i = 0; i < te.GetLength(0); i++)
        {
            System.Text.StringBuilder sb = 
                new System.Text.StringBuilder(rlabels[i]);
            
            int len = sb.Length;
            for (int j = 0; j < (8 - len); j++)
                sb.Append(' ');
            sb.Append(te[i,0].ToString("0.0000"));
            
            len = sb.Length;
            for (int j = 0; j < (16 - len); j++)
                sb.Append(' ');
            sb.Append(te[i,1].ToString("0.0000"));
            
            len = sb.Length;
            for (int j = 0; j < (32 - len); j++)
                sb.Append(' ');
            sb.Append(te[i,2].ToString("0.0000"));
            
            len = sb.Length;
            for (int j = 0; j < (48 - len); j++)
                sb.Append(' ');
            sb.Append(te[i,3].ToString("0.0000"));
            
            Console.Out.WriteLine(sb.ToString());
        }
    }
}

Output

P-value = 0.008299

          * * * Analysis of Variance * * *
degrees of freedom for the model                  18.0000
degrees of freedom for error                       8.0000
total (corrected) degrees of freedom              26.0000
sum of squares for the model                   2395.7290
sum of squares for error                         185.7763
total (corrected) sum of squares               2581.5052
model mean square                                133.0961
error mean square                                 23.2220
F-statistic                                        5.7315
p-value                                            0.0083
R-squared (in percent)                            92.8036
Adjusted R-squared (in percent)                   76.6116
est. standard deviation of the model error         4.8189
overall mean of y                                 98.9619
coefficient of variation (in percent)              4.8695

          * * * Variation Due to the Model * * *
Source	DF	Sum of Squares	Mean Square	Prob. of Larger F
A       2.0000  488.3675        10.5152         0.0058
B       2.0000  1090.6564       23.4832         0.0004
C       2.0000  49.1485         1.0582          0.3911
A*B     4.0000  142.5853        1.5350          0.2804
A*C     4.0000  32.3474         0.3482          0.8383
B*C     4.0000  592.6238        6.3800          0.0131