splineInterp¶

Compute a spline interpolant.

Synopsis¶

splineInterp (xdata, fdata)

Required Arguments¶

float xdata[] (Input): Array with ndata components containing the abscissas of the interpolation problem.
float fdata[] (Input): Array with ndata components containing the ordinates of the interpolation problem.

Return Value¶

The structure that represents the spline interpolant. If an interpolant cannot be computed, then None is returned.

Optional Arguments¶

order, int (Input)

The order of the spline subspace for which the knots are desired. This option is used to communicate the order of the spline subspace.

Default: order = 4, i.e., cubic splines

knots, float (Input)

This option requires the user to provide the knots.

Default: knots are selected by the function splineKnots using its defaults.

Description¶

Given the data points x = xdata, f = fdata, and the number n = ndata of elements in xdata and fdata, the default action of splineInterp computes a cubic (\(k = 4\)) spline interpolant s to the data using the default knot sequence generated by splineKnots.

The optional argument order allows the user to choose the order of the spline interpolant. The optional argument knots allows user specification of knots.

The function splineInterp is based on the routine SPLINT by de Boor (1978, p. 204).

First, splineInterp sorts the xdata vector and stores the result in x. The elements of the fdata vector are permuted appropriately and stored in f, yielding the equivalent data \((x_i, f_i)\) for \(i = 0\) to \(n − 1\).

The following preliminary checks are performed on the data. We verify that

\[\begin{split}\begin{array}{ll} x_i < x_{i+1} & i = 0, \ldots, n-2 \\ t_i < t_{i+k} & i = 0, \ldots, n-1 \\ t_i < t_{i+1} & i = 0, \ldots, n+k-2 \\ \end{array}\end{split}\]

The first test checks to see that the abscissas are distinct. The second and third inequalities verify that a valid knot sequence has been specified.

In order for the interpolation matrix to be nonsingular, we also check \(t_{k-1} \leq x_i \leq t_n\) for \(i = 0\) to \(n − 1\). This first inequality in the last check is necessary since the method used to generate the entries of the interpolation matrix requires that the k possibly nonzero B-splines at \(x_i\),

\[B_{j-k+1}, …, B_j\quad \text{where } j \text{ satisfies} \quad t_j ≤ x_i < t_{j+1}\]

be well-defined (that is, \(j − k + 1 \geq 0\)).

General conditions are not known for the exact behavior of the error in spline interpolation; however, if t and x are selected properly and the data points arise from the values of a smooth (say \(C^k\)) function f, i.e. \(f_j = f(x_j)\), then the error will behave in a predictable fashion. The maximum absolute error satisfies

\[\left\|f-s\right\|_{\left[t_{k-1},t_n\right]} \leq C \left\|f^{(k)}\right\|_{\left[t_{k-1},t_n\right]} |t|^k\]

where

\[|t| := \max_{i=k-1,\ldots,n-1} \left|t_{i+1} - t_i\right|\]

For more information on this problem, see de Boor (1978, Chapter 13) and his reference.

The return value for this function is the structure Imsl_d_spline. This structure contains all the information to determine the spline (stored as a linear combination of B-splines) that is computed by this function. For example, the following code sequence evaluates this spline at x and returns the value in y.

y = cubSplineValue (x, sp, 0)

Three spline interpolants of order 2, 3, and 5 are plotted. These splines use the default knots.

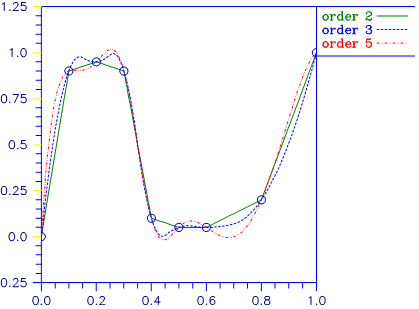
../../_images/Figure-ThreeSplineInterpolants.png

Figure 3.4 — Three Spline Interpolants

Examples¶

Example 1¶

In this example, a cubic spline interpolant to a function f is computed. The values of this spline are then compared with the exact function values. Since the default settings are used, the interpolant is determined by the “not-a-knot” condition (see de Boor 1978).

from __future__ import print_function
from numpy import *
from pyimsl.math.splineInterp import splineInterp
from pyimsl.math.splineValue import splineValue

# Define function


def F(x):
    return sin(15.0 * x)


# Set up a grid
ndata = 11
xdata = empty(ndata)
fdata = empty(ndata)
for i in range(0, ndata):
    xdata[i] = float(i) / (ndata - 1)
    fdata[i] = F(xdata[i])

# Compute cubic spline interpolant
sp = splineInterp(xdata, fdata)

# Print results
print("     x        F(x)     Interpolant     Error")
for i in range(0, 2 * ndata - 1):
    x = float(i) / (2 * ndata - 2)
    y = splineValue(x, sp)
    print('%6.3f  %10.3f   %10.3f   %10.4f' % (x, F(x), y, abs(F(x) - y)))

Output¶

     x        F(x)     Interpolant     Error
000       0.000        0.000       0.0000
050       0.682        0.809       0.1270
100       0.997        0.997       0.0000
150       0.778        0.723       0.0552
200       0.141        0.141       0.0000
250      -0.572       -0.549       0.0228
300      -0.978       -0.978       0.0000
350      -0.859       -0.843       0.0162
400      -0.279       -0.279       0.0000
450       0.450        0.441       0.0093
500       0.938        0.938       0.0000
550       0.923        0.903       0.0199
600       0.412        0.412       0.0000
650      -0.320       -0.315       0.0049
700      -0.880       -0.880       0.0000
750      -0.968       -0.938       0.0295
800      -0.537       -0.537       0.0000
850       0.183        0.148       0.0347
900       0.804        0.804       0.0000
950       0.994        1.086       0.0926
000       0.650        0.650       0.0000

Example 2¶

Recall that in the first example, a cubic spline interpolant to a function f is computed. The values of this spline are then compared with the exact function values. This example chooses to use a quadratic (\(k = 3\)) and a quintic \(k = 6\) spline interpolant to the data instead of the default values.

from __future__ import print_function
from numpy import *
from pyimsl.math.splineInterp import splineInterp
from pyimsl.math.splineValue import splineValue

# Define function


def F(x):
    return sin(15.0 * x)


# Set up a grid
ndata = 11
xdata = empty(ndata)
fdata = empty(ndata)
for i in range(0, ndata):
    xdata[i] = float(i) / (ndata - 1)
    fdata[i] = F(xdata[i])

for order in range(3, 7, 3):
    # Compute cubic spline interpolant
    sp = splineInterp(xdata, fdata, order=order)
    # Print results
    print("\nThe order of the spline is: ", order)
    print("     x        F(x)     Interpolant     Error")
    for i in range(int(ndata / 2), int(3 * ndata / 2)):
        x = float(i) / (2 * ndata - 2)
        y = splineValue(x, sp)
        print('%6.3f  %10.3f   %10.3f   %10.4f' % (x, F(x), y, abs(F(x) - y)))

Output¶

The order of the spline is:  3
     x        F(x)     Interpolant     Error
250      -0.572       -0.542       0.0299
300      -0.978       -0.978       0.0000
350      -0.859       -0.819       0.0397
400      -0.279       -0.279       0.0000
450       0.450        0.429       0.0210
500       0.938        0.938       0.0000
550       0.923        0.879       0.0433
600       0.412        0.412       0.0000
650      -0.320       -0.305       0.0149
700      -0.880       -0.880       0.0000
750      -0.968       -0.922       0.0459

The order of the spline is:  6
     x        F(x)     Interpolant     Error
250      -0.572       -0.573       0.0016
300      -0.978       -0.978       0.0000
350      -0.859       -0.856       0.0031
400      -0.279       -0.279       0.0000
450       0.450        0.448       0.0020
500       0.938        0.938       0.0000
550       0.923        0.922       0.0003
600       0.412        0.412       0.0000
650      -0.320       -0.322       0.0025
700      -0.880       -0.880       0.0000
750      -0.968       -0.959       0.0090

Warning Errors¶

IMSL_ILL_COND_INTERP_PROB The interpolation matrix is ill-conditioned. The solution might not be accurate.

Fatal Errors¶

`IMSL_DUPLICATE_XDATA_VALUES`	The xdata values must be distinct.
`IMSL_KNOT_MULTIPLICITY`	Multiplicity of the knots cannot exceed the order of the spline.
`IMSL_KNOT_NOT_INCREASING`	The knots must be nondecreasing.
`IMSL_KNOT_XDATA_INTERLACING`	The i-th smallest element of xdata (\(x_j\)) must satisfy \(t_j \leq x_j < t_{j+order}\) where t is the knot sequence.
`IMSL_XDATA_TOO_LARGE`	The array xdata must satisfy \(xdata_j \leq t_{ndata}\), for i = 1, …, ndata.
`IMSL_XDATA_TOO_SMALL`	The array xdata must satisfy \(xdata_j \geq t_{order-1}\), for i = 1, …, ndata.