besselJ0¶

Evaluates the real Bessel function of the first kind of order zero $J_0(x)$ .

Synopsis¶

besselJ0 (x)

Required Arguments¶

float x (Input): Point at which the Bessel function is to be evaluated.

Return Value¶

The value of the Bessel function

$J_0(x) = \frac{1}{\pi} \int_0^{\pi} \cos(x \sin \theta) d \theta$

If no solution can be computed, NaN is returned.

Description¶

Because the Bessel function $J_0(x)$ is oscillatory, its computation becomes inaccurate as $|x|$ increases.

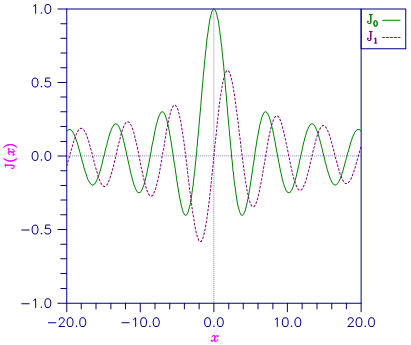
Figure 9.16 — Plot of $J_0(x)$ and $J_1(x)$

Example¶

The Bessel function $J_0(1.5)$ is evaluated.

from __future__ import print_function
from numpy import *
from pyimsl.math.besselJ0 import besselJ0

x = 1.5
ans = besselJ0(x)
print("J0(%f) = %f" % (x, ans))

Output¶

J0(1.500000) = 0.511828

Warning Errors¶

IMSL_LARGE_ABS_ARG_WARN $|x|$ should be less than $1/\sqrt{\varepsilon}$ where ɛ is the machine precision, to prevent the answer from being less accurate than half precision.

Fatal Errors¶

IMSL_LARGE_ABS_ARG_FATAL $|x|$ should be less than $1/\varepsilon$ where ɛ is the machine precision for the answer to have any precision.