fCdf¶

Evaluates the F distribution function.

Synopsis¶

fCdf (f, dfNumerator, dfDenominator)

Required Arguments¶

float f (Input): Point at which the F distribution function is to be evaluated.
float dfNumerator (Input): The numerator degrees of freedom. Argument dfNumerator must be positive.
float dfDenominator (Input): The denominator degrees of freedom. Argument dfDenominator must be positive.

Return Value¶

The probability that an F random variable takes a value less than or equal to the input point, f.

Description¶

Function fCdf evaluates the distribution function of a Snedecor’s F random variable with dfNumerator and dfDenominator. The function is evaluated by making a transformation to a beta random variable, then evaluating the incomplete beta function. If X is an F variate with \(\nu_1\) and \(\nu_2\) degrees of freedom and \(Y=(\nu_1 X)/(\nu_2+\nu_1 X)\), then Y is a beta variate with parameters \(p=\nu_1/2\) and \(q=\nu_2/2\). Function fCdf also uses a relationship between F random variables that can be expressed as

\[F_F(f|v_1, v_2) = 1 - F_F(1/f|v_2, v_1)\]

where \(F_F\) is the distribution function for an F random variable.

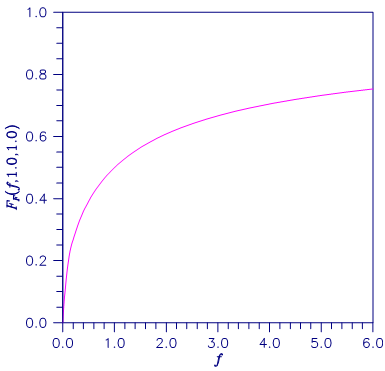
Figure 11.6 — Plot of \(F_F(f,1.0,1.0)\)

Example¶

This example finds the probability that an F random variable with one numerator and one denominator degree of freedom is greater than 648.

from __future__ import print_function
from numpy import *
from pyimsl.stat.fCdf import fCdf

f = 648.0
df_numerator = 1.0
df_denominator = 1.0
p = 1 - fCdf(f, df_numerator, df_denominator)
print("The probability that an F(1,1) variate is greater than 648 is %6.4f" % p)

Output¶

The probability that an F(1,1) variate is greater than 648 is 0.0250