cub_spline_tcb
Computes a tension-continuity-bias (TCB) cubic spline interpolant. This is also called a Kochanek-Bartels spline and is a generalization of the Catmull–Rom spline.
Synopsis
#include <imsl.h>
Imsl_f_ppoly *imsl_f_cub_spline_tcb (int ndata, float xdata[], float fdata[], ..., 0)
The type Imsl_d_ppoly function is imsl_d_cub_spline_tcb.
Required Arguments
int ndata (Input)
Number of data points.
Number of data points.
float xdata[] (Input)
Array with ndata components containing the abscissas of the interpolation problem.
Array with ndata components containing the abscissas of the interpolation problem.
float fdata[] (Input)
Array with ndata components containing the ordinates for the interpolation problem.
Array with ndata components containing the ordinates for the interpolation problem.
Return Value
A pointer to the structure that represents the interpolant. If an interpolant cannot be computed, NULL is returned. To release this space, use imsl_free.
Synopsis with Optional Arguments
#include <imsl.h>
Imsl_f_ppoly *imsl_f_cub_spline_tcb (int ndata, float xdata[], float fdata[],
IMSL_TENSION, float tension[],
IMSL_CONTINUITY, float continuity[],
IMSL_BIAS, float bias[],
IMSL_LEFT, double left,
IMSL_RIGHT, double right,
0)
Optional Arguments
IMSL_TENSION, float tension[] (Input)
Sets the tension values at the data points. The array tension is of length ndata and contains tension values in the interval [-1,1]. For each point, if the tension value is near +1 the curve is tightened at that point. If it is near -1, the curve is slack.
Default: All values of tension are zero.
Sets the tension values at the data points. The array tension is of length ndata and contains tension values in the interval [-1,1]. For each point, if the tension value is near +1 the curve is tightened at that point. If it is near -1, the curve is slack.
Default: All values of tension are zero.
IMSL_CONTINUITY, float continuity[] (Input)
Sets the continuity values at the data points. The array continuity is of length ndata and contains continuity values in the interval [-1,1]. For each point, if the continuity value is zero the curve is C1 at that point. Otherwise the curve has a corner at that point, but is still continuous (C0).
Default: All values of continuity are zero.
Sets the continuity values at the data points. The array continuity is of length ndata and contains continuity values in the interval [-1,1]. For each point, if the continuity value is zero the curve is C1 at that point. Otherwise the curve has a corner at that point, but is still continuous (C0).
Default: All values of continuity are zero.
IMSL_BIAS, float bias[] (Input)
Sets the bias values at the data points. The array bias is of length ndata and contains bias values in the interval [-1,1]. For each point, if the bias value is zero the left and right side tangents are equally weighted. If the value is near +1 the left-side tangent dominates. If the value is near -1 the right-side tangent dominates.
Default: All values of bias are zero.
Sets the bias values at the data points. The array bias is of length ndata and contains bias values in the interval [-1,1]. For each point, if the bias value is zero the left and right side tangents are equally weighted. If the value is near +1 the left-side tangent dominates. If the value is near -1 the right-side tangent dominates.
Default: All values of bias are zero.
IMSL_LEFT, double left (Input)
Sets the value of the tangent at the leftmost endpoint.
Default: left = 0.
Sets the value of the tangent at the leftmost endpoint.
Default: left = 0.
IMSL_RIGHT, double right (Input)
Sets the value of the tangent at the rightmost endpoint.
Default: right = 0.
Sets the value of the tangent at the rightmost endpoint.
Default: right = 0.
Description
The function imsl_f_cub_spline_tcb computes the Kochanek-Bartels spline, a piecewise cubic Hermite spline interpolant to a set of data points {xi, fi} for i = 0, …, ndata-1. The breakpoints of the spline are the abscissas. As with all of the univariate interpolation functions, the abscissas need not be sorted.
The {xi} values are the knots, so the i-th interval is [xi, xi+1]. (To simplify the explanation, it is assumed that the data points are given in increasing order.) The cubic Hermite interpolant in the i-th segment has a starting value of fi and an ending value of fi+1. Its incoming tangent is
where ti is the i-th tension value, ci is the i-th continuity value, and bi is the i-th bias value. Its outgoing tangent is
The optional arguments left and right are used at the endpoints i = 0 and i = ndata-1:
and
Both left and right default to zero.
The spline has a continuous first derivative (is C1) if at each data point the left and right tangents are equal. This is true if the continuity parameters, ci, are all zero. For any values of the parameters the spline is continuous (C0).
If ti = ci = bi = 0 for all i, then the curve is the Catmull-Rom spline.
The following chart shows the same data points interpolated with different parameter values. All of the tension, continuity and bias parameters are zero except for the labeled parameter, which has the indicated value at all data points.
Tension controls how sharply the spline bends at the data points. If tension is near +1, the curve tightens. If tension is near -1, the curve slackens.
The continuity parameter controls the continuity of the first derivative. If continuity is zero, the spline’s first derivative is continuous, so the spline is C1.
The bias parameter controls the weighting of the left and right tangents. If zero, the tangents are equally weighted. If the bias parameter is near +1, the left tangent dominates. If the bias parameter is near -1, the right tangent dominates.
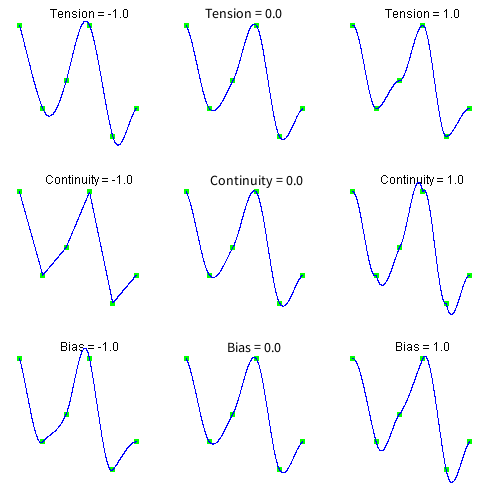
Figure 3, Data Points Interpolated with Different Parameter Values
Examples
Example 1
This example interpolates to a set of points. At x = 3 the continuity and tension parameters are -1. At all other points, they are zero. Interpolated values are then printed.
#include <imsl.h>
#include <stdio.h>
int main()
{
int m = 2, ndata = 6, i;
float x, y;
float xdata[] = { 0, 1, 2, 3, 4, 5 };
float fdata[] = { 5, 2, 3, 5, 1, 2 };
float continuity[] = { 0, 0, 0, -1, 0, 0 };
float tension[] = { 0, 0, 0, -1, 0, 0 };
Imsl_f_ppoly *ppoly;
ppoly = imsl_f_cub_spline_tcb(ndata, xdata, fdata,
IMSL_CONTINUITY, continuity,
IMSL_TENSION, tension,
0);
for (i = 0; i < m*(ndata - 1) + 1; i++) {
x = i / (float)m;
y = imsl_f_cub_spline_value(x, ppoly, 0);
printf(" %6.3f %10.4f\n", x, y);
}
if (ppoly)
imsl_free(ppoly);
}
Output
0.000 5.0000
0.500 3.4375
1.000 2.0000
1.500 2.1875
2.000 3.0000
2.500 3.6875
3.000 5.0000
3.500 2.1875
4.000 1.0000
4.500 1.2500
5.000 2.0000
Example 2
It is possible to use an interpolating spline for approximation by using an optimization function to compute its parameters. In this example a series of n interest rates, ri, for different maturities, xi, is given, {xi, ri} for i = 0, …, n-1. Since the dates are given on a widely varying time scale, the base 10 logarithm of the dates is used for interpolation.
A TCB spline is constructed using a subset of the given data points for knot locations, {pi , qi}, for i = 0, …, m-1. The p values are a subset of the log10 xi values. The q values are to be determined by the optimizer. The spline has non-zero values of the continuity parameter, ci, for i = 0, …, m-1.
The optimization problem finds the spline, , which interpolates the points {pi, qi} and has continuity parameters, c, and specified left and right parameters.
The optimization problem is
subject to the bounds, for all i,
The function constrained_nlp is used as the optimizer. The unknowns q, c, left and right are packed into the array x, respectively.
#include <imsl.h>
#include <stdio.h>
#include <math.h>
void fcn(int, double[], int, double *, int *);
double objective(double *, double *, double, double);
#define N_DATA 15
static int days[] = { 3, 31, 62, 94, 185, 367, 731, 1096, 1461, 1826, 2194,
2558, 2922, 3287, 3653 };
static double log_days[N_DATA];
static double rate[] = { 5.01772, 4.98284, 4.97234, 4.96157, 4.99058,
5.09389, 5.79733, 6.30595, 6.73464, 6.94816, 7.08807, 7.27527,
7.30852, 7.3979, 7.49015 };
/* Knots are set on a subset of the data points */
#define N_KNOTS 4
static double xknots[N_KNOTS];
static int subset[] = { 0, 5, 10, 14 };
#define Y_KNOTS 0
#define CONTINUITY (Y_KNOTS + N_KNOTS)
#define LEFT (CONTINUITY + N_KNOTS)
#define RIGHT (LEFT + 1)
#define N_VARIABLES (RIGHT + 1)
int main()
{
int n_constraints, ibtype, i;
double y;
double *x, xlb[N_VARIABLES], xub[N_VARIABLES];
double xguess[N_VARIABLES];
Imsl_d_ppoly *ppoly;
n_constraints = 0;
ibtype = 0;
for (i = 0; i < N_KNOTS; i++) {
xlb[Y_KNOTS + i] = 0.1; /* lower bound on rate */
xub[Y_KNOTS + i] = 10.0; /* upper bound on rate */
xlb[CONTINUITY + i] = -0.95; /* lower bound on continuity */
xub[CONTINUITY + i] = 0.95; /* upper bound on continuity */
}
/* Set bounds wide enough on LEFT and RIGHT so they are not binding */
xlb[LEFT] = -100.0; xub[LEFT] = 100.0;
xlb[RIGHT] = -100.0; xub[RIGHT] = 100.0;
for (i = 0; i < N_DATA; i++) {
log_days[i] = log10(days[i]);
}
for (i = 0; i < N_KNOTS; i++) {
xknots[i] = log_days[subset[i]];
xguess[Y_KNOTS + i] = rate[subset[i]];
xguess[CONTINUITY + i] = 0.0;
}
xguess[LEFT] = xguess[RIGHT] = 0.0;
/* Find the optimal curve */
x = imsl_d_constrained_nlp(fcn, n_constraints, 0, N_VARIABLES,
ibtype, xlb, xub,
IMSL_XGUESS, xguess,
IMSL_DIFFTYPE, 3,
0);
/* Report results */
ppoly = imsl_d_cub_spline_tcb(N_KNOTS, xknots, x,
IMSL_CONTINUITY, x + CONTINUITY,
IMSL_LEFT, x[LEFT],
IMSL_RIGHT, x[RIGHT],
0);
printf("Days Rate Curve Error\n");
for (i = 0; i < N_DATA; i++) {
y = imsl_d_cub_spline_value(log_days[i], ppoly, 0);
printf("%4d %6.3f %6.3f %6.3f\n",
days[i], rate[i], y, y - rate[i]);
}
printf("\n");
for (i = 0; i < N_KNOTS; i++) {
printf("continuity[%2d] = %6.3f\n", days[i], x[CONTINUITY + i]);
}
printf("\nleft = %6.3f\nright = %6.3f\n", x[LEFT], x[RIGHT]);
if (x)
imsl_free(x);
if (ppoly)
imsl_free(ppoly);
}
/* Function passed to imsl_d_constrained_nlp */
void fcn(int n, double x[], int iact, double *result, int *ierr)
{
if (iact == 0) {
*result = objective(x + Y_KNOTS, x + CONTINUITY, x[LEFT], x[RIGHT]);
}
}
/* Compute the objective function, the sum of squares error */
double objective(double *yknots, double *continuity,
double left, double right)
{
int i;
double y, diff, error;
Imsl_d_ppoly *ppoly;
ppoly = imsl_d_cub_spline_tcb(N_KNOTS, xknots, yknots,
IMSL_CONTINUITY, continuity,
IMSL_LEFT, left,
IMSL_RIGHT, right,
0);
error = 0.0;
for (i = 0; i < N_DATA; i++) {
y = imsl_d_cub_spline_value(log_days[i], ppoly, 0);
diff = y - rate[i];
error += diff * diff;
}
if (ppoly)
imsl_free(ppoly);
return error / N_DATA;
}
Output
Days Rate Curve Error
3 5.018 5.019 0.002
31 4.983 4.998 0.015
62 4.972 4.959 -0.013
94 4.962 4.951 -0.010
185 4.991 4.980 -0.011
367 5.094 5.084 -0.010
731 5.797 5.842 0.045
1096 6.306 6.340 0.034
1461 6.735 6.683 -0.052
1826 6.948 6.931 -0.017
2194 7.088 7.118 0.030
2558 7.275 7.240 -0.035
2922 7.309 7.332 0.023
3287 7.398 7.408 0.011
3653 7.490 7.479 -0.011
continuity[ 3] = 0.009
continuity[31] = -0.630
continuity[62] = -0.184
continuity[94] = -0.950
left = 0.534
right = 0.266