normal_cdf
Evaluates the standard normal (Gaussian) distribution function.
Synopsis
#include <imsl.h>
float imsl_f_normal_cdf (float x)
The type double function is imsl_d_normal_cdf.
Required Arguments
float x (Input)
Point at which the normal distribution function is to be evaluated.
Point at which the normal distribution function is to be evaluated.
Return Value
The probability that a normal random variable takes a value less than or equal to x.
Description
The function imsl_f_normal_cdf evaluates the distribution function, Φ, of a standard normal (Gaussian) random variable; that is,
The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.
The standard normal distribution (for which imsl_f_normal_cdf is the distribution function) has mean of 0 and variance of 1. The probability that a normal random variable with mean μ and variance σ2 is less than y is given by imsl_f_normal_cdf evaluated at (y − μ)/σ.
Φ(x) is evaluated by use of the complementary error function, imsl_f_erfc. The relationship is:
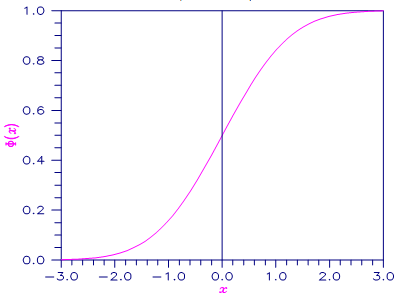
Figure 20, Plot of Φ(x)
Example
Suppose X is a normal random variable with mean 100 and variance 225. This example finds the probability that X is less than 90 and the probability that X is between 105 and 110.
#include <imsl.h>
int main()
{
float p, x1, x2;
x1 = (90.0-100.0)/15.0;
p = imsl_f_normal_cdf(x1);
printf("The probability that X is less than 90 is %6.4f\n\n", p);
x1 = (105.0-100.0)/15.0;
x2 = (110.0-100.0)/15.0;
p = imsl_f_normal_cdf(x2) - imsl_f_normal_cdf(x1);
printf("The probability that X is between 105 and 110 is %6.4f\n", p);
}
Output
The probability that X is less than 90 is 0.2525
The probability that X is between 105 and 110 is 0.1169