F_cdf
Evaluates the F distribution function.
Synopsis
#include <imsls.h>
float imsls_f_F_cdf (float f, float df_numerator, float df_denominator)
The type double function is imsls_d_F_cdf.
Required Arguments
float f (Input)
Point at which the F distribution function is to be evaluated.
Point at which the F distribution function is to be evaluated.
float df_numerator (Input)
The numerator degrees of freedom. Argument df_numerator must be positive.
The numerator degrees of freedom. Argument df_numerator must be positive.
float df_denominator (Input)
The denominator degrees of freedom. Argument df_denominator must be positive.
The denominator degrees of freedom. Argument df_denominator must be positive.
Return Value
The probability that an F random variable takes a value less than or equal to the input point, f.
Description
Function imsls_f_F_cdf evaluates the distribution function of a Snedecor’s F random variable with df_numerator and df_denominator. The function is evaluated by making a transformation to a beta random variable, then evaluating the incomplete beta function. If X is an F variate with ν1 and ν2 degrees of freedom and Y = (ν1X)/(ν2 + ν1X), then Y is a beta variate with parameters p = ν1/2 and q= ν2/2. Function imsls_f_F_cdf also uses a relationship between F random variables that can be expressed as
FF(f|v1, v2) = 1 - FF(1/f|v2, v1)
where FF is the distribution function for an F random variable.
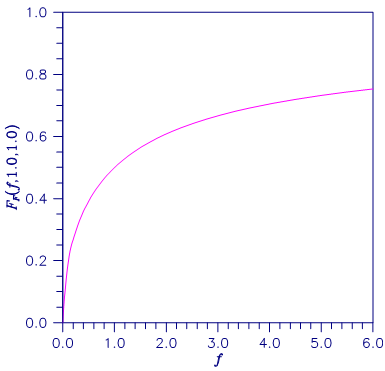
Figure 16, Plot of FF(f, 1.0, 1.0)
Example
This example finds the probability that an F random variable with one numerator and one denominator degree of freedom is greater than 648.
#include <imsls.h>
#include <stdio.h>
int main()
{
float F = 648.0, df_numerator = 1.0;
float df_denominator = 1.0, p;
p = 1.0 - imsls_f_F_cdf(F,df_numerator, df_denominator);
printf("The probability that an F(%1.0f,%1.0f) variate"
"is greater than %3.0f is %6.4f.\n", df_numerator,
df_denominator, F, p);
}
Output
The probability that an F(1,1) variate is greater than 648 is 0.0250.