non_central_t_cdf
Evaluates the noncentral Student’s t distribution function.
Synopsis
#include <imsls.h>
floatimsls_f_non_central_t_cdf(float t, int df, float delta)
The type double function is imsls_d_non_central_t_cdf.
Required Arguments
float t (Input)
Argument for which the noncentral Student’s t distribution function is to be evaluated.
Argument for which the noncentral Student’s t distribution function is to be evaluated.
intdf (Input)
Number of degrees of freedom of the noncentral Student’s t distribution. Argument df must be greater than or equal to 0.0.
Number of degrees of freedom of the noncentral Student’s t distribution. Argument df must be greater than or equal to 0.0.
float delta (Input)
The noncentrality parameter.
The noncentrality parameter.
Return Value
The probability that a noncentral Student’s t random variable takes a value less than or equal to t.
Description
Function imsls_f_non_central_t_cdf evaluates the distribution function F of a noncentral t random variable with df degrees of freedom and noncentrality parameter delta; that is, with v = df, δ = delta, and t0 = t,
where Γ(⋅) is the gamma function. The value of the distribution function at the point t0 is the probability that the random variable takes a value less than or equal to t0.
The noncentral t random variable can be defined by the distribution function above, or alternatively and equivalently, as the ratio of a normal random variable and an independent chi-squared random variable. If w has a normal distribution with mean δ and variance equal to one, u has an independent chi-squared distribution with v degrees of freedom, and
then x has a noncentral t distribution with degrees of freedom and noncentrality parameter δ.
The distribution function of the noncentral t can also be expressed as a double integral involving a normal density function (see, for example, Owen 1962, page 108). The function TNDF uses the method of Owen (1962, 1965), which uses repeated integration by parts on that alternate expression for the distribution function.
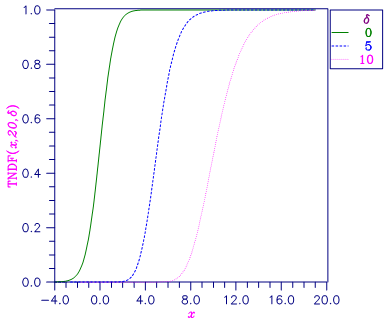
Figure 21, Noncentral Student’s t Distribution Function
Example
Suppose t is a noncentral t random variable with 6 degrees of freedom and noncentrality parameter 6. In this example, we find the probability that t is less than 12.0. (This can be checked using the table on page 111 of Owen 1962, with η = 0.866, which yields λ = 1.664.)
#include <imsls.h>
#include <stdio.h>
int main()
{
int df = 6;
float t = 12.0, delta = 6.0, p;
p = imsls_f_non_central_t_cdf(t, df, delta);
printf("The probability that t is less than %2.0f "
"is %6.4f.\n", t, p);
}
Output
The probability that T is less than 12.0 is 0.9501