poly_regression
Performs a polynomial least-squares regression.
Synopsis
#include <imsls.h>
float *imsls_f_poly_regression (int n_observations, float x[], float y[], int degree, ..., 0)
The type double function is imsls_d_poly_regression.
Required Arguments
int n_observations (Input)
Number of observations.
Number of observations.
float x[] (Input)
Array of length n_observations containing the independent variable.
Array of length n_observations containing the independent variable.
float y[] (Input)
Array of length n_observations containing the dependent variable.
Array of length n_observations containing the dependent variable.
int degree (Input)
Degree of the polynomial.
Degree of the polynomial.
Return Value
A pointer to the array of size degree + 1 containing the coefficients of the fitted polynomial. If a fit cannot be computed, NULL is returned.
Synopsis with Optional Arguments
#include <imsls.h>
float *imsls_f_poly_regression (int n_observations, float x[], float y[], int degree,
IMSLS_WEIGHTS, float weights[],
IMSLS_SSQ_POLY, float **ssq_poly,
IMSLS_SSQ_POLY_USER, float ssq_poly[],
IMSLS_SSQ_POLY_COL_DIM, int ssq_poly_col_dim,
IMSLS_SSQ_LOF, float **ssq_lof,
IMSLS_SSQ_LOF_USER, float ssq_lof[],
IMSLS_SSQ_LOF_COL_DIM, int ssq_lof_col_dim,
IMSLS_X_MEAN, float *x_mean,
IMSLS_X_VARIANCE, float *x_variance,
IMSLS_ANOVA_TABLE, float **anova_table,
IMSLS_ANOVA_TABLE_USER, float anova_table[]
IMSLS_DF_PURE_ERROR, int *df_pure_error,
IMSLS_SSQ_PURE_ERROR, float *ssq_pure_error,
IMSLS_RESIDUAL, float **residual,
IMSLS_RESIDUAL_USER, float residual[],
IMSLS_POLY_REGRESSION_INFO, Imsls_f_poly_regression **poly_info,
IMSLS_RETURN_USER, float coefficients[],
0)
Optional Arguments
IMSLS_WEIGHTS, float weights[] (Input)
Array with n_observations components containing the array of weights for the observation.
Default: weights[] = 1
Array with n_observations components containing the array of weights for the observation.
Default: weights[] = 1
IMSLS_SSQ_POLY, float **ssq_poly (Output)
Address of a pointer to the internally allocated array containing the sequential sums of squares and other statistics. Row i corresponds to xi, i = 0, ..., degree − 1, and the columns are described as follows:
Address of a pointer to the internally allocated array containing the sequential sums of squares and other statistics. Row i corresponds to xi, i = 0, ..., degree − 1, and the columns are described as follows:
Column | Description |
|---|---|
0 | degrees of freedom |
1 | Sums of squares |
2 | F-statistic |
3 | p-value |
IMSLS_SSQ_POLY_USER, float ssq_poly[] (Output)
Storage for array ssq_poly is provided by the user. See IMSLS_SSQ_POLY.
Storage for array ssq_poly is provided by the user. See IMSLS_SSQ_POLY.
IMSLS_SSQ_POLY_COL_DIM, int ssq_poly_col_dim (Input)
Column dimension of ssq_poly.
Default: ssq_poly_col_dim = 4
Column dimension of ssq_poly.
Default: ssq_poly_col_dim = 4
IMSLS_SSQ_LOF, float **ssq_lof (Output)
Address of a pointer to the internally allocated array containing the lack-of-fit statistics. Row icorresponds to xi, i = 0, ..., degree − 1, and the columns are described in the following table:
Address of a pointer to the internally allocated array containing the lack-of-fit statistics. Row icorresponds to xi, i = 0, ..., degree − 1, and the columns are described in the following table:
Column | Description |
|---|---|
0 | degrees of freedom |
1 | lack-of-fit sums of squares |
2 | F-statistic for testing lack-of-fit for a polynomial model of degree i |
3 | p-value for the test |
IMSLS_SSQ_LOF_USER, float ssq_lof[] (Output)
Storage for array ssq_lof is provided by the user. See IMSLS_SSQ_LOF.
Storage for array ssq_lof is provided by the user. See IMSLS_SSQ_LOF.
IMSLS_SSQ_LOF_COL_DIM, int ssq_lof_col_dim (Input)
Column dimension of ssq_lof.
Default: ssq_lof_col_dim = 4
Column dimension of ssq_lof.
Default: ssq_lof_col_dim = 4
IMSLS_X_MEAN, float *x_mean (Output)
Mean of x.
Mean of x.
IMSLS_X_VARIANCE, float *x_variance (Output)
Variance of x.
Variance of x.
IMSLS_ANOVA_TABLE, float **anova_table (Output)
Address of a pointer to the array containing the analysis of variance table.
Address of a pointer to the array containing the analysis of variance table.
Column | Description |
|---|---|
0 | degrees of freedom for the model |
1 | degrees of freedom for error |
2 | total (corrected) degrees of freedom |
3 | sum of squares for the model |
4 | sum of squares for error |
5 | total (corrected) sum of squares |
6 | model mean square |
7 | error mean square |
8 | overall F-statistic |
9 | p-value |
10 | R2 (in percent) |
11 | adjusted R2 (in percent) |
12 | estimate of the standard deviation |
13 | overall mean of y |
14 | coefficient of variation (in percent) |
Note that the p‑value is returned as 0.0 when the value is so small that all significant digits have been lost.
IMSLS_ANOVA_TABLE_USER, float anova_table[] (Output)
Storage for anova_table is provided by the user. See IMSLS_ANOVA_TABLE.
Storage for anova_table is provided by the user. See IMSLS_ANOVA_TABLE.
IMSLS_DF_PURE_ERROR, int *df_pure_error (Output)
If specified, the degrees of freedom for pure error are returned in df_pure_error.
If specified, the degrees of freedom for pure error are returned in df_pure_error.
IMSLS_SSQ_PURE_ERROR, float *ssq_pure_error (Output)
If specified, the sums of squares for pure error are returned in ssq_pure_error.
If specified, the sums of squares for pure error are returned in ssq_pure_error.
IMSLS_RESIDUAL, float **residual (Output)
Address of a pointer to the array containing the residuals.
Address of a pointer to the array containing the residuals.
IMSLS_RESIDUAL_USER, float residual[] (Output)
Storage for array residual is provided by the user. See IMSLS_RESIDUAL.
Storage for array residual is provided by the user. See IMSLS_RESIDUAL.
IMSLS_POLY_REGRESSION_INFO, Imsls_f_poly_regression **poly_info (Output)
Address of a pointer to an internally allocated structure containing the information about the polynomial fit required as input for IMSL function imsls_f_poly_prediction.
Address of a pointer to an internally allocated structure containing the information about the polynomial fit required as input for IMSL function imsls_f_poly_prediction.
IMSLS_RETURN_USER, float coefficients[] (Output)
If specified, the least-squares solution for the regression coefficients is stored in array coefficients of size degree + 1 provided by the user.
If specified, the least-squares solution for the regression coefficients is stored in array coefficients of size degree + 1 provided by the user.
Description
Function imsls_f_poly_regression computes estimates of the regression coefficients in a polynomial (curvilinear) regression model. In addition to the computation of the fit, imsls_f_poly_regression computes some summary statistics. Sequential sums of squares attributable to each power of the independent variable (stored in ssq_poly) are computed. These are useful in assessing the importance of the higher order powers in the fit. Draper and Smith (1981, pp. 101−102) and Neter and Wasserman (1974, pp. 278−287) discuss the interpretation of the sequential sums of squares. The statistic R2 is the percentage of the sum of squares of y about its mean explained by the polynomial curve. Specifically,
where
is the fitted yvalue at xi and is the mean of y. This statistic is useful in assessing the overall fit of the curve to the data. R2 must be between 0 and 100 percent, inclusive. R2 = 100 percent indicates a perfect fit to the data.
Estimates of the regression coefficients in a polynomial model are computed using orthogonal polynomials as the regressor variables. This reparameterization of the polynomial model in terms of orthogonal polynomials has the advantage that the loss of accuracy resulting from forming powers of the x-values is avoided. All results are returned to the user for the original model (power form).
Function imsls_f_poly_regression is based on the algorithm of Forsythe (1957). A modification to Forsythe’s algorithm suggested by Shampine (1975) is used for computing the polynomial coefficients. A discussion of Forsythe’s algorithm and Shampine’s modification appears in Kennedy and Gentle (1980, pp. 342−347).
Examples
Example 1
A polynomial model is fitted to data discussed by Neter and Wasserman (1974, pp. 279−285). The data set contains the response variable y measuring coffee sales (in hundred gallons) and the number of self-service coffee dispensers. Responses for 14 similar cafeterias are in the data set. A graph of the results is also given.
#include <imsls.h>
#define DEGREE 2
#define NOBS 14
int main()
{
float *coefficients;
float x[] = {0.0, 0.0, 1.0, 1.0, 2.0, 2.0, 4.0,
4.0, 5.0, 5.0, 6.0, 6.0, 7.0, 7.0};
float y[] = {508.1, 498.4, 568.2, 577.3, 651.7, 657.0, 755.3,
758.9, 787.6, 792.1, 841.4, 831.8, 854.7, 871.4};
coefficients = imsls_f_poly_regression (NOBS, x, y, DEGREE, 0);
imsls_f_write_matrix("Least-Squares Polynomial Coefficients",
DEGREE + 1, 1, coefficients,
IMSLS_ROW_NUMBER_ZERO,
0);
}
Output
Least-Squares Polynomial Coefficients
0 503.3
1 78.9
2 -4.0
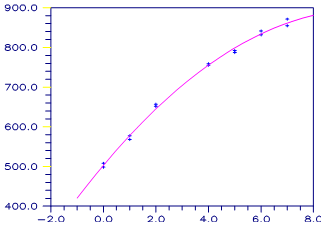
Figure 1, A Polynomial Fit
Example 2
This example is a continuation of the initial example. Here, many optional arguments are used.
#include <imsls.h>
#define DEGREE 2
#define NOBS 14
int main()
{
int iset = 1, dfpe;
float *coefficients, *anova_table, sspe, *ssqpoly, *ssqlof;
float x[] = {
0.0, 0.0, 1.0, 1.0, 2.0, 2.0, 4.0, 4.0, 5.0, 5.0, 6.0, 6.0,
7.0, 7.0
};
float y[] = {
508.1, 498.4, 568.2, 577.3, 651.7, 657.0, 755.3, 758.9, 787.6,
792.1, 841.4, 831.8, 854.7, 871.4
};
char *coef_rlab[2];
char *coef_clab[] = {" ", "intercept", "linear", "quadratic"};
char *stat_clab[] = {" ", "Degrees of\nFreedom", "Sum of\nSquares",
"\nF-Statistic", "\np-value"};
char *anova_rlab[] = {
"degrees of freedom for regression",
"degrees of freedom for error",
"total (corrected) degrees of freedom",
"sum of squares for regression",
"sum of squares for error",
"total (corrected) sum of squares",
"regression mean square",
"error mean square", "F-statistic",
"p-value", "R-squared (in percent)",
"adjusted R-squared (in percent)",
"est. standard deviation of model error",
"overall mean of y",
"coefficient of variation (in percent)"
};
coefficients = imsls_f_poly_regression(NOBS, x, y, DEGREE,
IMSLS_SSQ_POLY, &ssqpoly,
IMSLS_SSQ_LOF, &ssqlof,
IMSLS_ANOVA_TABLE, &anova_table,
IMSLS_DF_PURE_ERROR, &dfpe,
IMSLS_SSQ_PURE_ERROR, &sspe,
0);
imsls_write_options(-1, &iset);
imsls_f_write_matrix("Least Squares Polynomial Coefficients",
1, DEGREE + 1, coefficients,
IMSLS_COL_LABELS, coef_clab,
0);
coef_rlab[0] = coef_clab[2];
coef_rlab[1] = coef_clab[3];
imsls_f_write_matrix("Sequential Statistics", DEGREE, 4,
ssqpoly,
IMSLS_COL_LABELS, stat_clab,
IMSLS_ROW_LABELS, coef_rlab,
IMSLS_WRITE_FORMAT, "%3.1f%8.1f%6.1f%6.4f",
0);
imsls_f_write_matrix("Lack-of-Fit Statistics", DEGREE, 4,
ssqlof,
IMSLS_COL_LABELS, stat_clab,
IMSLS_ROW_LABELS, coef_rlab,
IMSLS_WRITE_FORMAT, "%3.1f%8.1f%6.1f%6.4f",
0);
imsls_f_write_matrix("* * * Analysis of Variance * * *\n", 15,
1, anova_table,
IMSLS_ROW_LABELS, anova_rlab,
IMSLS_WRITE_FORMAT, "%9.2f",
0);
}
Output
Least Squares Polynomial Coefficients
intercept linear quadratic
503.3 78.9 -4.0
Sequential Statistics
Degrees of Sum of
Freedom Squares F-Statistic p-value
linear 1.0 220644.2 3415.8 0.0000
quadratic 1.0 4387.7 67.9 0.0000
Lack-of-Fit Statistics
Degrees of Sum of
Freedom Squares F-Statistic p-value
linear 5.0 4793.7 22.0 0.0004
quadratic 4.0 405.9 2.3 0.1548
* * * Analysis of Variance * * *
degrees of freedom for regression 2.00
degrees of freedom for error 11.00
total (corrected) degrees of freedom 13.00
sum of squares for regression 225031.94
sum of squares for error 710.55
total (corrected) sum of squares 225742.48
regression mean square 112515.97
error mean square 64.60
F-statistic 1741.86
p-value 0.00
R-squared (in percent) 99.69
adjusted R-squared (in percent) 99.63
est. standard deviation of model error 8.04
overall mean of y 710.99
coefficient of variation (in percent) 1.13
Warning Errors
IMSLS_CONSTANT_YVALUES | The y values are constant. A zero-order polynomial is fit. High order coefficients are set to zero. |
IMSLS_FEW_DISTINCT_XVALUES | There are too few distinct x values to fit the desired degree polynomial. High order coefficients are set to zero. |
IMSLS_PERFECT_FIT | A perfect fit was obtained with a polynomial of degree less than degree. High order coefficients are set to zero. |
Fatal Errors
IMSLS_NONNEG_WEIGHT_REQUEST_2 | All weights must be nonnegative. |
IMSLS_ALL_OBSERVATIONS_MISSING | Each (x, y) point contains NaN. There are no valid data. |
IMSLS_CONSTANT_XVALUES | The x values are constant. |