multi_crosscorrelation

CNL Stat : Time Series and Forecasting : multi_crosscorrelation

Synopsis

Required Arguments

Return Value

Synopsis with Optional Arguments

Optional Arguments

Description

Example

more...

Computes the multichannel cross-correlation function of two mutually stationary multichannel time series.

Synopsis

#include <imsls.h>

float *imsls_f_multi_crosscorrelation (int n_observations_x, int n_channel_x, float x[], int n_observations_y, int n_channel_y, float y[], int lagmax, ..., 0)

The type double function is imsls_d_multi_crosscorrelation.

Required Arguments

int n_observations_x (Input)
Number of observations in each channel of the first time series x. n_observations_x must be greater than or equal to two.

int n_channel_x (Input)
Number of channels in the first time series x. n_channel_x must be greater than or equal to one.

float x[] (Input)
Array of length n_observations_x by n_channel_x containing the first time series.

int n_observations_y (Input)
Number of observations in each channel of the second time series y. n_observations_y must be greater than or equal to two.

int n_channel_y (Input)
Number of channels in the second time series y. n_channel_y must be greater than or equal to one.

float y[] (Input)
Array of length n_observations_y by n_channel_y containing the second time series.

int lagmax (Input)
Maximum lag of cross-covariances and cross-correlations to be computed. lagmax must be greater than or equal to one and less than the minimum of n_observations_x and n_observations_y.

Return Value

Pointer to an array of length n_channel_x× n_channel_y × (2 × lagmax + 1) containing the cross-correlations between the channels of x and y. The m-th element of this array contains the cross-correlation between channel i of the x series and channel j of the y series at lag (k-lagmax) where

i = 1, …, n_channel_x

j = 1, …, n_channel_y

k = 0, 1, …, 2*lagmax, and

m = (n_channel_x*n_channel_y*k +(i*n_channel_x+ j))

To release this space, use imsls_free. If no solution can be computed, NULL is return.

Synopsis with Optional Arguments

#include <imsls.h>

float *imsls_f_multi_crosscorrelation(int n_observations_x, int n_channel_x, float x[], int n_observations_y, int n_channel_y, float y[], int lagmax,

IMSLS_PRINT_LEVEL, int iprint,

IMSLS_INPUT_MEANS, float *x_mean_in, float *y_mean_in,

IMSLS_OUTPUT_MEANS, float **x_mean_out, float **y_mean_out,

IMSLS_OUTPUT_MEANS_USER, float x_mean_out[], float y_mean_out[],

IMSLS_VARIANCES, float **x_variance, float **y_variance,

IMSLS_VARIANCES_USER, float x_variance[], float y_variance[],

IMSLS_CROSS_COVARIANCES, float **cross_covariances,

IMSLS_CROSS_COVARIANCES_USER, float cross_covariances[],

IMSLS_RETURN_USER, float crosscorrelations[],

Optional Arguments

IMSLS_PRINT_LEVEL, int iprint (Input)
Printing option.

iprint	Action
0	No printing is performed.
1	Prints the means and variances.
2	Prints the means, variances, and cross-covariances.
3	Prints the means, variances, cross-covariances, and cross-correlations.

Default = 0.

IMSLS_INPUT_MEANS, float *x_mean_in, float *y_mean_in (Input)
If specified, x_mean_in is an array of length n_channel_x containing the user input of the estimate of the means of the channels of x and y_mean_in is an array of length n_channel_y containing the user input of the estimate of the means of the channels of y.

IMSLS_OUTPUT_MEANS, float **x_mean_out, float **y_mean_out (Output)
If specified, x_mean_out is the address of a pointer to an array of length n_channel_x containing the means of the channels of x and y_mean_out is the address of a pointer to an array of length n_channel_y containing the means of the channels of y.

IMSLS_OUTPUT_MEANS_USER, float x_mean_out[], float y_mean_out[] (Output)
If specified, x_mean_out is an array of length n_channel_x containing the means of the channels of x and y_mean_out is an array of length n_channel_y containing the means of the channels of y. See IMSLS_OUTPUT_MEANS.

IMSLS_VARIANCES, float **x_variance, float **y_variance (Output)
If specified, x_variance is the address of a pointer to an array of length n_channel_x containing the variances of the channels of x and y_variance is the address of a pointer to an array of length n_channel_y containing the variances of the channels of y.

IMSLS_VARIANCES_USER, float x_variance[], float y_variance[] (Output)
If specified, x_variance is an array of length n_channel_x containing the variances of the channels of x and y_variance is an array of length n_channel_y containing the variances of the channels of y. See IMSLS_VARIANCES.

IMSLS_CROSS_COVARIANCES, float **cross_covariances (Output)
Address of a pointer to an array of length n_channel_x × n_channel_y × (2×lagmax + 1) containing the cross-covariances between the channels of x and y. The mth element of this array contains the cross-covariance between channel i of the x series and channel j of the y series at lag (k−lagmax) where

i = 1, …, n_channel_x

j = 1, …, n_channel_y

k = 0, 1, …, 2*lagmax, and

m = (n_channel_x*n_channel_y*k +(i*n_channel_x+ j)).

IMSLS_CROSS_COVARIANCES_USER, float cross_covariances (Output)
If specified, cross_covariances is an array of length n_channel_x × n_channel_y × (2×lagmax + 1) containing the cross-covariances between the channels of x and y. See IMSLS_CROSS_COVARIANCES.

IMSLS_RETURN_USER, float crosscorrelations[] (Output)
If specified, crosscorrelations is a user-specified array of length n_channel_x × n_channel_y × (2×lagmax + 1) containing the cross-correlations between the channels of x and y. See Return Value.

Description

Function imsls_f_multi_crosscorrelation estimates the multichannel cross-correlation function of two mutually stationary multichannel time series. Define the multichannel time series X by

X = (X1, X2, ..., Xp)

where

Xj = (X1j, X2j, ..., Xnj)T, j = 1, 2, ..., p

with n = n_observations_x and p = n_channel_x. Similarly, define the multichannel time series Y by

Y = (Y1, Y2, ..., Yq)

where

Yj = (Y1j, Y2j, ..., Ymj)T, j = 1, 2, ..., q

with m = n_observations_y and q = n_channel_y. The columns of X and Y correspond to individual channels of multichannel time series and may be examined from a univariate perspective. The rows of X and Y correspond to observations of p-variate and q-variate time series, respectively, and may be examined from a multivariate perspective. Note that an alternative characterization of a multivariate time series X considers the columns to be observations of the multivariate time series while the rows contain univariate time series. For example, see Priestley (1981, page 692) and Fuller (1976, page 14).

Let

be the row vector containing the means of the channels of X. In particular,

where for j = 1, 2, …, p

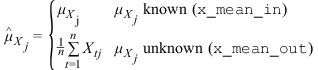
Let

be similarly defined for the means of the channels of Y. The cross-covariance of lag k between channel i of X and channel j of Y is estimated by

where i = 1, …, p, j = 1, …, q, and K = lagmax. The summation on t extends over all possible cross-products with N equal to the number of cross-products in the sum

Let

be the row vector consisting of the estimated variances of the channels of X. In particular,

where

Let

be similarly defined. The cross-correlation of lag k between channel i of X and channel j of Y is estimated by

Example

Consider the Wolfer Sunspot Data (Y) (Box and Jenkins 1976, page 530) along with data on northern light activity (X1) and earthquake activity (X2) (Robinson 1967, page 204) to be a three-channel time series. Function imsls_f_multi_crosscorrelation is used to compute the cross-covariances and cross-correlations between X1 and Y and between X2 and Y with lags from −10 through 10.

#include <imsls.h>

#include <stdio.h>

int main () {

int i, lagmax, nobsx, nchanx, nobsy, nchany;

float x[100 * 2], y[100], *result = NULL, *xvar = NULL, *yvar = NULL,

*xmean = NULL, *ymean = NULL, *ccv = NULL;

float data[100][4];

char line[20];

nobsx = nobsy = 100;

nchanx = 2;

nchany = 1;

lagmax = 10;

imsls_f_data_sets (8, IMSLS_X_COL_DIM, 4, IMSLS_RETURN_USER, data, 0);

for (i = 0; i < 100; i++)

{

y[i] = data[i][1];

x[i * 2] = data[i][2];

x[i * 2 + 1] = data[i][3];

}

result =

imsls_f_multi_crosscorrelation (nobsx, nchanx, &x[0], nobsy, nchany,

&y[0], lagmax, IMSLS_VARIANCES, &xvar,

&yvar, IMSLS_OUTPUT_MEANS, &xmean, &ymean,

IMSLS_CROSS_COVARIANCES, &ccv, 0);

imsls_f_write_matrix ("Channel means of x", 1, nchanx, xmean, 0);

imsls_f_write_matrix ("Channel variances of x", 1, nchanx, xvar, 0);

imsls_f_write_matrix ("Channel means of y", 1, nchany, ymean, 0);

imsls_f_write_matrix ("Channel variances of y", 1, nchany, yvar, 0);

printf ("\nMultichannel cross-covariance between x and y\n");

for (i = 0; i < (2 * lagmax + 1); i++)

{

sprintf (line, "Lag K = %d", i - lagmax);

imsls_f_write_matrix (line, nchanx, nchany,

&ccv[nchanx * nchany * i], 0);

}

printf ("\nMultichannel cross-correlation between x and y\n");

for (i = 0; i < (2 * lagmax + 1); i++)

{

sprintf (line, "Lag K = %d", i - lagmax);

imsls_f_write_matrix (line, nchanx, nchany,

&result[nchanx * nchany * i], 0);

}

Output

Channel means of x

1 2

63.43 97.97

Channel variances of x

1 2

2644 1978

Channel means of y

46.94

Channel variances of y

1384

Multichannel cross-covariance between x and y

Lag K = -10

1 -20.51

2 70.71

Lag K = -9

1 65.02

2 38.14

Lag K = -8

1 216.6

2 135.6

Lag K = -7

1 246.8

2 100.4

Lag K = -6

1 142.1

2 45.0

Lag K = -5

1 50.70

2 -11.81

Lag K = -4

1 72.68

2 32.69

Lag K = -3

1 217.9

2 -40.1

Lag K = -2

1 355.8

2 -152.6

Lag K = -1

1 579.7

2 -213.0

Lag K = 0

1 821.6

2 -104.8

Lag K = 1

1 810.1

2 55.2

Lag K = 2

1 628.4

2 84.8

Lag K = 3

1 438.3

2 76.0

Lag K = 4

1 238.8

2 200.4

Lag K = 5

1 143.6

2 283.0

Lag K = 6

1 253.0

2 234.4

Lag K = 7

1 479.5

2 223.0

Lag K = 8

1 724.9

2 124.5

Lag K = 9

1 925.0

2 -79.5

Lag K = 10

1 922.8

2 -279.3

Multichannel cross-correlation between x and y

Lag K = -10

1 -0.01072

2 0.04274

Lag K = -9

1 0.03400

2 0.02305

Lag K = -8

1 0.1133

2 0.0819

Lag K = -7

1 0.1290

2 0.0607

Lag K = -6

1 0.07431

2 0.02718

Lag K = -5

1 0.02651

2 -0.00714

Lag K = -4

1 0.03800

2 0.01976

Lag K = -3

1 0.1139

2 -0.0242

Lag K = -2

1 0.1860

2 -0.0923

Lag K = -1

1 0.3031

2 -0.1287

Lag K = 0

1 0.4296

2 -0.0633

Lag K = 1

1 0.4236

2 0.0333

Lag K = 2

1 0.3285

2 0.0512

Lag K = 3

1 0.2291

2 0.0459

Lag K = 4

1 0.1248

2 0.1211

Lag K = 5

1 0.0751

2 0.1710

Lag K = 6

1 0.1323

2 0.1417

Lag K = 7

1 0.2507

2 0.1348

Lag K = 8

1 0.3790

2 0.0752

Lag K = 9

1 0.4836

2 -0.0481

Lag K = 10

1 0.4825

2 -0.1688