Evaluates the real beta function β(x, y).
Synopsis
#include <imsl.h>
float imsl_f_beta (float x, float y)
The type double procedure is imsl_d_beta.
Required Arguments
float x
(Input)
Point at which the beta function is to be evaluated. It must be
positive.
float y
(Input)
Point at which the beta function is to be evaluated. It must be
positive.
Return Value
The value of the beta function β (x, y). If no result can be computed, NaN is returned.
Description
The beta function, β (x, y), is defined to be
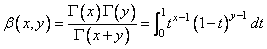
The beta function requires that x > 0 and y > 0. It underflows for large arguments.
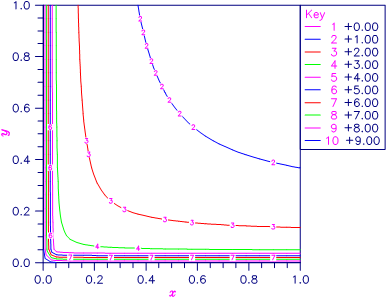
Figure 9- 5 Plot of β(x,y)
Example
Evaluate the beta function β (0.5, 0.2).
#include
<imsl.h>
main()
{
float x = 0.5;
float y = 0.2;
float ans;
ans =
imsl_f_beta(x, y);
printf("beta(%f,%f) = %f\n", x, y,
ans);
}
Output
beta(0.500000,0.200000) = 6.268653
Alert Errors
IMSL_BETA_UNDERFLOW The arguments must not be so large that the result underflows.
Fatal Errors
IMSL_ZERO_ARG_OVERFLOW One of the arguments is so close to zero that the result overflows.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |