Computes the integral of a cubic spline.

Synopsis

#include <imsl.h>

float imsl_f_cub_spline_integral (float a, float b, Imsl_f_ppoly *ppoly)

The type double function is imsl_d_cub_spline_integral.

Required Arguments

float a   (Input)

float b   (Input)
Endpoints for integration.

Imsl_f_ppoly *ppoly   (Input)
Pointer to the piecewise polynomial structure that represents the cubic spline.

Return Value

The integral from a to b of the cubic spline. If no value can be computed, then NaN is returned.

Description

The function imsl_f_cub_spline_integral computes the integral of a cubic spline from a to b.

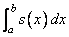
Example

In this example, a cubic spline interpolant to a function f is computed. The values of the integral of this spline are then compared with the exact integral values. Since the default settings are used, the interpolant is determined by the “not-a-knot” condition (see de Boor 1978).

#include <imsl.h>
#include <stdio.h>
#include <math.h>

#define NDATA   21
                                /* Define function */
#define F(x)    (float)(sin(15.0*x))
                                /* Integral from 0 to x */
#define FI(x)   (float)((1.-cos(15.0*x))/15.)

main()
{
    int                 i;
    float               fdata[NDATA], xdata[NDATA], x, y;
    Imsl_f_ppoly        *pp;
                                /* Set up a grid */
    for (i = 0;  i < NDATA;  i++) {
        xdata[i] = (float)i /((float)(NDATA-1));
        fdata[i] = F(xdata[i]);
    }
                                /* Compute cubic spline interpolant */
    pp = imsl_f_cub_spline_interp_e_cnd (NDATA, xdata, fdata, 0);
                                /* Print results */
    printf("     x         FI(x)      Interpolant   Integral Error\n");
    for (i = NDATA/2;  i < 3*NDATA/2;  i++){
        x = (float) i /(float)(2*NDATA-2);
        y = imsl_f_cub_spline_integral(0.0, x, pp);
        printf("  %6.3f  %10.3f   %10.3f   %10.4f\n", x, FI(x), y,
                                                   fabs(FI(x)-y));
        }
}

Output

  x         FI(x)   Interpolant   Integral Error
0.250       0.121        0.121       0.0001
0.275       0.104        0.104       0.0001
0.300       0.081        0.081       0.0001
0.325       0.056        0.056       0.0001
0.350       0.033        0.033       0.0001
0.375       0.014        0.014       0.0002
0.400       0.003        0.003       0.0002
0.425       0.000        0.000       0.0002
0.450       0.007        0.007       0.0002
0.475       0.022        0.022       0.0001
0.500       0.044        0.044       0.0001
0.525       0.068        0.068       0.0001
0.550       0.092        0.092       0.0001
0.575       0.113        0.113       0.0001
0.600       0.127        0.128       0.0001
0.625       0.133        0.133       0.0001
0.650       0.130        0.130       0.0001
0.675       0.118        0.118       0.0001
0.700       0.098        0.098       0.0001
0.725       0.075        0.075       0.0001
0.750       0.050        0.050       0.0001

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260