.p>.CMCH4.DOC!GAUSS_QUAD_RULE;gauss_quad_rule
Computes a Gauss, Gauss-Radau, or Gauss-Lobatto quadrature rule with various classical weight functions.
Synopsis
#include <imsl.h>
void imsl_f_gauss_quad_rule (int n, float weights[], float points[], ¼, 0)
The type double procedure is imsl_d_gauss_quad_rule.
Required Arguments
int n
(Input)
Number of quadrature points.
float weights[]
(Output)
Array of length n containing the quadrature weights.
float points[]
(Output)
Array of length n containing quadrature points. The default
action of this routine is to produce the Gauss Legendre points and weights.
Synopsis with Optional Arguments
#include <imsl.h>
void
imsl_f_gauss_quad_rule (int
n,
float
weights[], float points[],
IMSL_CHEBYSHEV_FIRST,
IMSL_CHEBYSHEV_SECOND,
IMSL_HERMITE,
IMSL_COSH,
IMSL_JACOBI, float
alpha,
float
beta,
IMSL_GEN_LAGUERRE, float
alpha,
IMSL_FIXED_POINT, float a,
IMSL_TWO_FIXED_POINTS, float a, float b,
0)
Optional Arguments
IMSL_CHEBYSHEV_FIRST
Compute
the Gauss points and weights using the weight function
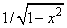
on the interval (−1, 1).
IMSL_CHEBYSHEV_SECOND
Compute
the Gauss points and weights using the weight function
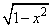
on the interval (−1, 1).
IMSL_HERMITE
Compute
the Gauss points and weights using the weight function exp (−x2) on the
interval (−¥, ¥).
IMSL_COSH
Compute
the Gauss points and weights using the weight function 1 ∕ (cosh (x)) on the
interval (−¥, ¥).
IMSL_JACOBI, float alpha, float beta
(Input)
Compute the Gauss points and weights using the weight function
(1 − x)a (1 +
x)b
on the interval (−1,
1).
IMSL_GEN_LAGUERRE, float alpha
(Input)
Compute the Gauss points and weights using the weight function exp
(−x)xa on the interval
(0, ¥).
IMSL_FIXED_POINT, float a
(Input)
Compute the Gauss-Radau points and weights using the specified weight
function and the fixed point a. This formula will integrate polynomials
of degree less than 2n − 1 exactly.
IMSL_TWO_FIXED_POINTS, float a, float b
(Input)
Compute the Gauss-Lobatto points and weights using the specified
weight function and the fixed points a and b. This formula will
integrate polynomials of degree less than 2n − 2 exactly.
Description
The function imsl_f_gauss_quad_rule produces the points and weights for the Gauss, Gauss-Radau, or Gauss-Lobatto quadrature formulas for some of the most popular weights. The default weight is the weight function identically equal to 1 on the interval (−1, 1). In fact, it is slightly more general than this suggests, because the extra one or two points that may be specified do not have to lie at the endpoints of the interval. This function is a modification of the subroutine GAUSSQUADRULE (Golub and Welsch 1969).
In the default case, the function returns points in x = points and weights in w = weights so that
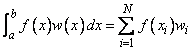
for all functions f that are polynomials of degree less than 2n.
If the keyword IMSL_FIXED_POINT is specified, then one of the above xi is equal to a. Similarly, if the keyword IMSL_TWO_FIXED_POINTS is specified, then two of the components of x are equal to a and b. In general, the accuracy of the above quadrature formula degrades when n increases. The quadrature rule will integrate all functions f that are polynomials of degree less than 2n − F, where F is the number of fixed points.
Examples
Example 1
The three-point Gauss Legendre quadrature points and weights are computed and used to approximate the integrals
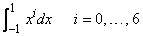
Notice that the integrals are exact for the first six monomials, but that the last approximation is in error. In general, the Gauss rules with k points integrate polynomials with degree less than 2k exactly.
#include <math.h>
#include
<imsl.h>
#define QUADPTS 3
#define
POWERS 7
main()
{
int i, j;
float weights[QUADPTS], points[QUADPTS],
s[POWERS];
/* Produce the Gauss Legendre
*/
/* quadrature points */
imsl_f_gauss_quad_rule (QUADPTS,
weights, points, 0);
/*
integrate the functions
*/
/* 1, x, ..., pow(x,POWERS-1) */
for(i = 0; i <
POWERS; i++) {
s[i] =
0.0;
for(j = 0; j <
QUADPTS; j++)
{
s[i] +=
weights[j]*imsl_fi_power(points[j],
i);
}
}
printf("The integral from -1 to 1 of pow(x, i)
is\n");
printf("Function
Quadrature Exact\n\n");
for(i = 0;
i < POWERS; i++){
float z;
z =
(1-i%2)*2./(i+1.);
printf("pow(x,
%d) %10.3f %10.3f\n", i, s[i],
z);
}
}
Output
The integral from -1 to 1 of pow(x, i)
is
Function
Quadrature Exact
pow(x,
0)
2.000 2.000
pow(x,
1)
0.000 0.000
pow(x,
2)
0.667 0.667
pow(x,
3)
0.000 0.000
pow(x,
4)
0.400 0.400
pow(x,
5)
0.000 0.000
pow(x,
6)
0.240 0.286
Example 2
The three-point Gauss Laguerre quadrature points and weights are computed and used to approximate the integrals
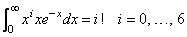
Notice that the integrals are exact for the first six monomials, but that the last approximation is in error. In general, the Gauss rules with k points integrate polynomials with degree less than 2k exactly.
#include <math.h>
#include
<imsl.h>
#define QUADPTS 3
#define
POWERS 7
main()
{
int i, j;
float weights[QUADPTS], points[QUADPTS],
s[POWERS],
z;
/* Produce the Gauss Legendre
*/
/* quadrature points */
imsl_f_gauss_quad_rule (QUADPTS,
weights, points,
IMSL_GEN_LAGUERRE, 1.0,
0);
/* Integrate the functions
*/
/* 1, x, ..., pow(x,POWERS-1) */
for(i = 0; i <
POWERS; i++) {
s[i] =
0.0;
for(j = 0; j <
QUADPTS;
j++){
s[i]
+= weights[j]*imsl_fi_power(points[j],
i);
}
}
printf("The integral from 0 to infinity of pow(x,
i)*x*exp(x) is\n");
printf("Function
Quadrature Exact\n\n");
for(z = 1.0, i =
0; i < POWERS;
i++){
z *=
(i+1);
printf("pow(x,
%d) %10.3f %10.3f \n", i,
s[i], z);
}
}
Output
The integral from 0 to infinity of pow(x, i)*x*exp(x)
is
Function
Quadrature Exact
pow(x,
0)
1.000 1.000
pow(x,
1)
2.000 2.000
pow(x,
2)
6.000 6.000
pow(x,
3)
24.000 24.000
pow(x,
4)
120.000 120.000
pow(x,
5)
720.000 720.000
pow(x,
6)
4896.000 5040.000
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |